Material Science - Juniper Publishers
Abstract
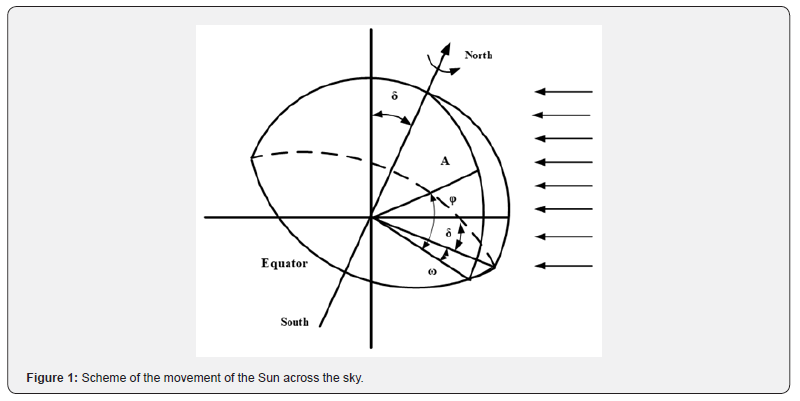
Analyzing the geographical location and climatic conditions of Turkmenistan, we conclude that solar energy is a priority among all renewable sources since the duration of sunny days in the country is from 270 to 320 days a year. Development, creation of large-scale solar power plants and use in remote desert regions of Turkmenistan is an urgent problem. The article considers the possibilities of creating a solar power plant based on a tower-type layout. The modes of the optical system in the natural and climatic conditions of Turkmenistan are calculated using a mathematical model, the coefficient of efficiency of using the mirror surface of the installation and the distribution of the level of instantaneous local values are determined. Figure 1 shows the movement of the Sun in the sky, which varies depending on the time of year. The results of the study show that the maximum increase in the energy efficiency coefficient can be achieved with the location of solar panels perpendicular to solar radiation with the dense placement of heliostats on the north side of the tower, then energy efficiency will increase by 25-40% in summer and 10-15% in winter.
Keywords: Solar energy; Tower solar power plant; Efficiency coefficient; Mirror surface; Heliostat; Optical system; Turkmenistan
Introduction
In the 21st century, humanity faced an acute problem of fuel for the power supply of various industrial and agricultural facilities. The reserves of minerals on Earth are not unlimited, the use of nuclear energy entails the danger of accidents, man-made disasters, and problems with the disposal of production waste. Against this background, the widespread use of renewable energy resources (RES) is of great interest. Turkmenistan, due to its geographical location and climatic features, is interested in the development of these energy sources.
The Law of Turkmenistan “On Renewable Energy Sources” regulates the relations between the state, producers and consumers, as well as the process of supplying equipment, installations and technologies for the use of renewable energy sources [1,2]. The Law outlines the main goals of using RES, in particular, reducing the growth of anthropogenic pressures on the environment and countering climate change, improving the quality of life and maintaining public health by reducing the growth of planetary pollution. The introduction of renewable energy resources into the fuel and energy complex will reduce the cost of transporting electricity, reduce the anthropogenic load on the environment and improve the social and living conditions of residents in remote areas, in this case, residents of the Karakum desert zone. All this undoubtedly indicates the extreme relevance of this topic [1-3]. The potential of solar energy is a ball of hydrogen and helium, in which continuous thermonuclear reactions occur, as a result of which energy is released with a temperature of t≈ 6000 o and radiant energy of 18000 billion kW, while the energy intensity on the Earth’s surface is 70-80 thousand kW / m2. But the intensity of solar radiation on the Earth’s surface depends on the natural and climatic features of the area, geographic latitude, air transparency, time of day and year, as well as altitude above sea level [3]. The gross potential of solar energy in the territory of Turkmenistan is estimated per square meter in the range from 1687.7 to 1897.2 kWh/m2 per year, the technical potential for heat production is from 1177.1 to 1296.78 kWh/m2 per year.
The amount of solar energy supplied to a horizontal surface varies depending on the natural and climatic conditions of the country’s region. The duration of sunshine at any point depends on the length of the day, cloudiness and increases from approaching the equator. However, the latitudinal distribution of sunshine is often disturbed due to the presence of clouds due to the peculiarities of atmospheric circulation, and fogs in coastal zones. The duration of sunshine on the territory of Turkmenistan varies depending on the season of the year in hours: in winter from 107 to 120, in spring 146-282, in summer 331-352, and in autumn 160-293. The total duration of sunshine is 2680 hours, the average daylight time is 8 hours 40 minutes per year. The average sunrise time is 6 hours 50 minutes, the average sunset time is 17 hours 25 minutes.
The potential of solar energy is the sum of the duration of solar radiation during the year and the total solar radiation incident on a horizontal surface. It is possible to increase the amount of solar radiation by changing the angle of inclination of the receiving surface. The maximum magnification will be achieved if the solar tracking panels are placed perpendicular to the solar radiation [3]. In the efficient operation of a solar power plant, the most important role is played by the optimal orientation of the solar radiation receiver with three main angles: the latitude of the receiver location φ , the hour angle ω and the declination of the Sun δ, shown in figure 1 for clarity.
Figure 1 shows the latitude, φ is the angle between the line connecting point A with the center of the Earth 0, and its projection onto the equatorial plane. The hour angle, ω, is the angle measured in the equatorial plane between the projection of the line OA and the projection of the line connecting the centers of the Earth and the Sun. Angle ω = 0 at solar noon; per hour corresponds to 15°. The declination of the sun, δ, is the angle between the line connecting the centers of the Earth and the Sun and its projection onto the equatorial plane. The declination of the sun continuously changes throughout the year: from -23°27’ on the day of the winter solstice on December 22 to +23°27’ on the day of the summer solstice on June 22 and is equal to zero on the days of the spring and autumn equinoxes (March 21 and September 23) [3-6].
Based on this, the position of the Sun relative to the Earth continuously changes during the year and day, then in order to obtain the maximum possible power density of solar radiation, the angles must also change accordingly, therefore, continuous tracking of the movement of the Sun is necessary. However, as numerous studies have shown, the use of automated tracking systems increases the cost of solar installation. In this regard, stationary solar receivers are the most effective for low-power solar installations. The method with a fixed orientation of the panels for the entire period of operation has the lowest energy efficiency, but it is easy to implement.
Using innovative methods, it is possible to calculate the level of specific insolation for each day of the month of the year under average meteorological conditions. The goals and objectives of the study are to carry out an overview analysis of modern structures, develop a model of a solar tower station, and optimize the operating modes of the optical system of a solar power station using computer simulation. The scientific novelty lies in the calculation of the efficiency factor for the use of a mirror surface in the heliostat field of a solar tower power plant in Turkmenistan. The calculation method is based on theoretical calculations using geometric and optical elements to create a model of a tower solar station.
The day in the middle of the month was considered a typical day. Multiplying the specific daily energy of solar radiation by the number of days in a month, we obtain the specific monthly energy of solar radiation.
Solar Electric Station of Tower Type (TSPS)
The design of the solar power tower type consists of a tower of various heights depending on the power (from 18 to 24 m), and a black water tank, which is located at the top of the tower. Black color serves for better heat absorption. Outside there is a turbogenerator, from which pumps supply water to the tank. Around the tower are mirrors – heliostats (Figure 2) [5,6].

The principle of operation of heliostats is related to the general mechanism for tracking the position of the sun in the sky. The main task of the tracking mechanism is to ensure that heliostat mirrors located in a certain area around the station reflect the sun’s rays exactly into the steam generator. The power of a tower solar power plant depends on the number of installed heliostats. As a result, the concentration of solar radiation increases from the number of heliostats and the water temperature in the steam generator reaches up to 700°C, while powerful steam is formed that rotates the electric generator, electricity is generated and the efficiency of such solar power plants reaches up to 20% [5,6]./p>
Research Methodology
Mathematical research methods can reduce the search time, help in making adequate decisions, and increase the reliability of the entire system and the efficiency of the station [7-10].
One of the main tasks of designing solar tower stations is the rational arrangement of the optical system of mirrors. For their smooth operation, it is necessary to take into account a number of requirements, factors and limitations [10]. For example, to achieve a high radiation flux concentration factor, it is necessary to place a large number of mirror reflectors in the smallest possible area. However, the dense arrangement of specular reflectors in the specular field leads to their mutual shading [7-10]. Thus, the loss of solar radiation flux in the optical system really affects the efficient operation of solar power plants, as well as the operation of solar furnaces.
To implement the task, a mathematical model was compiled that allows a comparative analysis and selection of layout options for the optical system of a tower-type solar power plant [10]. For the rational use of optical systems, determining the efficiency, and the efficiency of using the mirror surface of heliostats in a tower solar power plant, a mathematical model has been compiled [7- 10]. When developing a computational scheme for a mathematical model of the operation of the fields of mirror reflectors of a solar power plant, we took into account the continuous coincidence of the normal vector N to the mirror and the bisector of the plane angle, which is located between the heliostat and the sun and the heliostat and the receiver.
The position of the mirror reflector of the heliostat is determined by the vectors Nj, the ratios of the vectors are shown in the geometric diagram (Figure 1). Applying the dot product rule for the i-th heliostat at a given time, is equal to the vector cosine of half the angle:


Here’s the expression for the cosine of a double angle:

cozy cosine coefficient is the efficiency optical system of solar
SES.
From equation (1) and (3) we write:

Now, for the numerical implementation of the algorithm for calculating the values of the efficiency of the optical system of a solar station on a computer, we present the vector expression of the cosine coefficient of equation (4) in the form of a coordinate expression [7-10].
In the local Cartesian coordinate system XYZ, the components of the unit vector of the Sun have the form:

where X is the south side; Y is the east side; Z is the zenith; β-latitude of the location of the BSES, β=37 - 43 s.l. - for Turkmenistan; δ- the angle of inclination of the terrain is determined by the formula:

Ω- the hour angle is determined by the formula:

Where ω-the angular velocity of the Earth’s rotation is determined by the formula:

where τ- solar time, in hours, calculated from astronomical noon.
From figure 1, the components of a single vector in the XYZ coordinate system for individual heliostats are determined by the following formula:

In this formula, we make the following simplifications and assume that the first heliostat is located on the XZ plane, then the aiming coordinates focused at the tower point for all heliostats will be:

Where H is the height of the tower, H = 70 cm; r is the radius of the heliostat field, r = 110 cm.
Then in equation (9) we obtain the components Rxl in the following form

We determine the coefficient η for all mirror reflectors of a heliostat of a tower type, thus, we find the efficiency of using heliostats according to the formula:

Equation (11) shows that the efficiency factor for using the mirror surface η of heliostats depends on the angular variables and the distribution of its values over the field is uniquely determined by linear coordinates [7-10].
Research Results and Conclusion
In this research work, we analyzed the results of optimizing and modeling the operating modes of the optical systems of solar furnaces and a power plant based on solar energy using the developed and built mock-up of a tower-type power plant.
Mathematical modeling of the operating modes of the optical system of the specified power plant has been carried out. The coefficient of efficiency of using the mirror surface η was determined for all heliostats. Figure 1 and the mathematical model show that the quantitative and qualitative indicators of the distribution of instantaneous local values change depending on the position of the sun in the sky. The obtained results of the mathematical model confirm the efficiency of using the mirror field of heliostats for different times of the day. The distribution of instantaneous local values is constantly changing in different periods of the operation of the optical system..
a) As a result of calculations and observations, we conclude that the maximum increase in the energy efficiency coefficient can be achieved in summer by 25-40%, and in winter by 10-15%, these results are obtained under the condition that the heliostats are located perpendicular to the solar radiation and the heliostats are densely placed on the north side of the tower.
To Know more about Juniper Online Journal Material Science
Click here: https://juniperpublishers.com/jojms/index.php
To Know more about our Juniper Publishers
Click here: https://juniperpublishers.com/index.php





No comments:
Post a Comment