A Note on Multivariate Granger Causality Measure in Time Series - Juniper Publishers

 Biostatistics and Biometrics - Juniper Publishers

Abstract

In this short communication, we introduce a class of multivariate time series models associated with autoregressive-moving average scheme. A choice for a non-negative multivariate Granger causality measure based on conditional linear dependence and feedback between time series is suggested for the model.

Introduction

We consider multivariate processes in discrete time t,

Each of these processes includes m jointly distributed random variables. The symbol ⊕ denotes the concatenation of vectors. Let Xt(p) be a 1*pm random vector for each t, so that

the following models

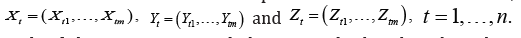
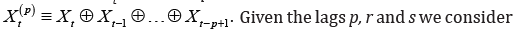
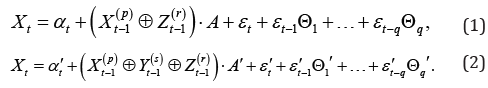
where 1,,qΘΘ and 1,,q′′ΘΘ are m*m real matrices. Compared to the odels (6) and (7) in [1], we introduce a structure of error vectors that has a finite order q moving average representation. Consider an example, suppose p=r=s=q=1, m=2 at time t,

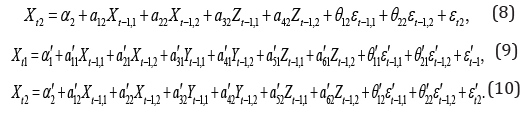
Assume that the processes Yt, Zt are jointly multivariate Gaussian, hence, Xt is also a multivariate Gaussian process. In the model, Gaussian assumptions hold, all variables are Gaussian distributed. Also, the error vectors are assumed to be uncorrelated with regressor vectors [2,3].

Concluding Remark

We introduce lags of error vector in the model since the history might have a direct influence on the current and the future. Moreover, the extend model has some nice properties. The past of unlocalizable information from error vectors can be used to predict the behavior of The model might capture direct influence, indirect influence, internal influence and unlocalizable influence.

There does not exit yet a formal definition of multivariate Granger formula in the literature for the models (1) and (2). Following the idea of [2], we formulate a non-negative multivariate causality measure for the model. Our formulation is based on conditional linear dependence and feedback between time series proposed by [3]

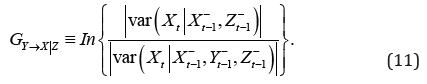
where Xt-1- denotes the history of X up to time t-1 Our choice is motivated from the discussion in [2, p.306] taking into account the moving average representation of error vector and a source of information given by Z. Note that multivariate G causality in (11) depends on the conditional variance Var(.|.) measure, see [3] for more details for the procedure to compute (11).

In summary, a generalized multivariate time series model is introduced based on the work of [1] and [4]. We note that conditional linear dependence and feedback between time series can be used to measure multivariate Granger causality for the proposed model.

To Know more about Biostatistics and Biometrics

Click here: https://juniperpublishers.com/bboaj/index.php

To Know more about our Juniper Publishers

Click here: https://juniperpublishers.com/index.php