Biostatistics and Biometrics Open Access Journal
We review the exponentiated generalized (EG) T-X family of distributions and propose some further developments of this class of distributions [1].
AMS subject classification: 35Q92, 92D30, 92D25.
Keywords:T-XW family of distributions; Transmuted family of distributions; Exponentiated
Abbrevations: EG: exponentiated generalized; QRTM: Quadratic Rank Transmutation Map;
Introduction
Transmuted family of distributions
According to the quadratic rank transmutation map (QRTM) approach in Shaw W, et al. [2], the CDF of the transmuted family of distributions is given by
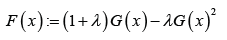
Where, 11λ−≤≤ and ()Gx is the CDF of the base distribution. When 0λ= we get the CDF of the base distribution
Remark 1.1. The PDF of the transmuted family of distributions is obtained by differentiating the CDF above.
A plethora of results discussing properties and applications of this class of distributions have appeared in the literature, and for examples see Faton Merovci, et al. [3] and Muhammad Shuaib Khan, et al [4].
T-XW family of distributions
This family of distributions is a generalization of the beta-generated family of distributions first proposed by Eugene et al. [5]. In particular, let ()rt be the PDF of the random variable T∈[a,b] ,−∞ ≤a< b ≤ ∞ and let WF((x)) be a monotonic and absolutely continuous function of the CDF F(x) of any random variable .X The CDF of a new family of distributions defined by Alzaatreh et al. [6] is given by
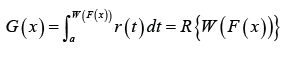
Where R(⋅) is the CDF of the random variable T and a≥ 0
Remark 1.2. The PDF of the T-X(W) family of distributions is obtained by differentiating the CDF above
Remark 1.3. When we set W(F(x)):=-ln(1-F(x)) then we use the term “T-X Family of Distributions” to describe all sub-classes of the T-X(W) family of distributions induced by the weight function W(x):=-ln(1-x) A description of different weight functions that are appropriate given the support of the random variable T is discussed in Alzaatreh A, et al. [6]
A plethora of results studying properties and application of the T-X(W) family of distributions have appeared in the literature, and the research papers, assuming open access, can be easily obtained on the web via common search engines, like Google, etc.
T-Transmuted X family of distributions
This class of distributions appeared in Jayakumar K, et al. [7]. In particular the CDF admits the following integral representation for a≥0
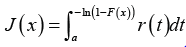
Where ()rt is the PDF of the random variable T and ()Fx is the transmuted CDF of the random variable ,Xthat is,
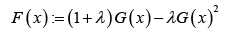
Where -1≤λ≤1 and ()Gx is the CDF of the base distribution.
Remark 1.4. The PDF of the T-Transmuted X family of distributions is obtained by differentiating the CDF above.
The exponentiated generalized (EG) T-X family of distributions
This class of distributions appeared in Suleman Nasiru, et al. [1]. In particular the CDF admits the following integral representation
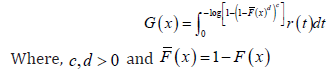
Remark 1.5. Note that if we set 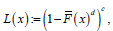 where ,0cd> and ()()1,FxFx=− then ()Lx gives the CDF of the exponentiated generalized class of distributions [8]
where ,0cd> and ()()1,FxFx=− then ()Lx gives the CDF of the exponentiated generalized class of distributions [8]
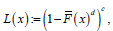 where ,0cd> and ()()1,FxFx=− then ()Lx gives the CDF of the exponentiated generalized class of distributions [8]
where ,0cd> and ()()1,FxFx=− then ()Lx gives the CDF of the exponentiated generalized class of distributions [8]Further developments
In this section, inspired by quantile generated probability distributions and the T transmuted X family of distributions [6,9], we propose some new extensions of the exponentiated generalized (EG) T-X family of distributions. We give the CDF of these new class of distributions, only in integral form. However, the CDF and PDF can be obtained explicitly by applying Theorem 2.2 and Theorem 2.3, respectively.
The TqX− family of distributions
Definition 2.1. Let V be any function such that the following holds:

Theorem 2.2. The CDF of the TqX− family induced by V is given by ()()()KxQVFx
Proof. Follows from the previous definition and noting that 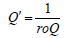
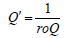
Theorem 2.3. The PDF of the TqX− family induced by V is given
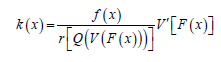
Proof. ,k=K′, 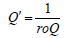 F′=f and K is given by Theorem 2.2
F′=f and K is given by Theorem 2.2
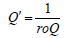 F′=f and K is given by Theorem 2.2
F′=f and K is given by Theorem 2.2
Remark 2.4. When the support of T is [),,a∞ where 0,a≥ we can take V as follows
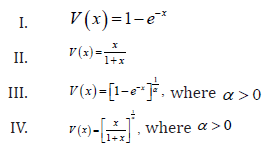
Remark 2.5. When the support of T is (),,−∞∞we can take V as follows
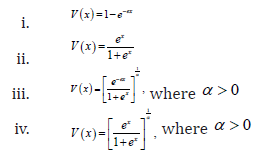
Definition 2.6. A random variable W (say) is said to be transmuted exponentiated generalized
distributed if the CDF is given by
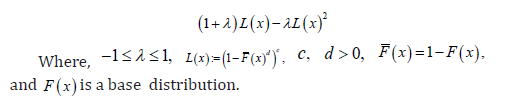
Some EG Tq transmuted X family of distributions
In what follows we assume the random variable T has PDF ()rt and quantile function ().Qt We also assume the random variable X has transmuted CDF
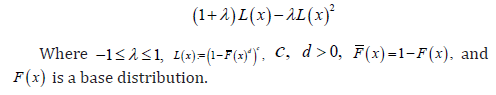
Families of EG Tq-transmuted X distributions of type I
The CDF has the following integral representation for α>0 and a≥0
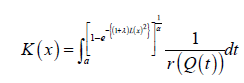
Families of EG Tq transmuted X distributions of type II
The CDF has the following integral representation for α>0 and a≥0
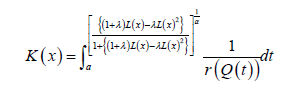
Families of EG Tq transmuted X distributions of Type III
The CDF has the following integral representation for 0α>
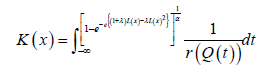
To Know More About Biostatistics and Biometrics Open Access Journal Please click on: https://juniperpublishers.com/bboaj/index.php




No comments:
Post a Comment