Soft robotics could loosely be described as the
engineering science of expanded dexterity through controllable
flexibility. The exploitation of controllable compliance through the
judicious choice of soft flexible members, as opposed to a finite number
of rigid kinematic joints, can result in greater dexterity without
compromising simplicity. One example is the replacement of segmented
mechanical legs with simple compliant material eruciform prolegs. To
achieve this in robotics, without introducing additional mechanical
joints, mobile surfaces with switchable coefficients of friction is
essential. This paper explains how, using silicone based smart
materials, the rapid alternation between kinematic and static friction
(stiction) may be achieved.
Introduction
Stiction (sometimes referred to as “stick-slip”) is a
word construction derived from friction and sticking. It represents the
forces due to static friction which manifests itself as a cohesion
force threshold which must be overcome to enable relative motion between
otherwise stationary objects in contact [1]. Following the onset of
movement, resistance to motion is provided exclusively by dynamic
friction. In engineering, stiction is usually considered to be a problem
[2]. However, in certain applications, stiction can be deliberately
implemented to advantage, as in the case of soft robotics where movement
is to be achieved through controlled sliding rather than rolling or
crawling. It is not easy to make a clear distinction between adhesion
and stiction. Both are related to inter molecular viscoelastic effects
and both are influenced by surface roughness. Adhesion (for example
magneto adhesion and electro adhesion) concerns the application of an
astrictive force which causes prehension whereas magnetostriction and
electrostriction pertain to the control of friction though a magnetic or
electric field respectively. Should it not be possible to sustain post
contact retention on lifting, then adhesion properties are absent. If,
despite this, the frictional coefficient is still controllable by means
of some external influence, then stiction is present.
The coefficient of static friction μs
denotes the necessary frictional force between two surfaces in order to
maintain two objects relative to one another immobile (1).

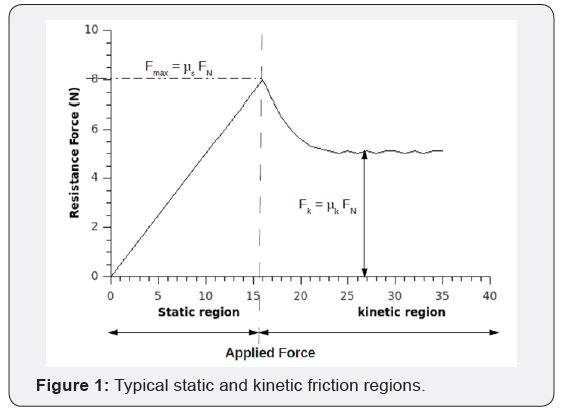
Once the applied force exceeds the maximum static
frictional force, sliding will commence. The force due to kinetic
friction (2) always opposes the direction of motion.

In expressions (1) and (2) FN is the force (usually due to gravity, FN
= m g) normal to the direction of motion. The surfaces of highly
polished planar objects tend to adhere to one another. This is often
attributed to electrostatic and/or Van der Waals forces. After
overcoming the initial stiction forces, relative motion occurs, and the
resistance shifts into the kinetic region as shown in Figure 1. Should
the movement direction be reversed, then a degree of positional
hysteresis will be experienced.
FN is a function of gravity and is otherwise only dependent
on mass. However, FN can be increased by the application of
additional force, though this is not necessarily advantageous.
What is important is the relationship between μs and μk.

In order to increase the relationship in (3), the mechanical
characteristics of one or both contacting material surfaces must
be precisely controlled. There are several relevant factors here.
Frictional Materials
Before introducing magnetically and electrically controllable
friction, it pays to consider the frictional coefficients of general
engineering materials. These are commonly available in almost
any mechanical engineering textbook [3]. The values given are
usually in the range 0 (no friction) to 1 (the frictional force is
equal to the normal force FN). Mechanically compliant materials
such as rubbers demonstrate some of the highest frictional
coefficients. In fact, silicone rubbers can have frictional
coefficients higher than unity [4]. What is required is a manner
in which these coefficients can be changed by means of an
external influence.
Compliance is the inverse of stiffness or the potential of a
surface to elastically change its geometry to comply with a
different topology. The ability to switch between two elastic
states is the basis of shape memory materials [5]. In the form of
a practical device, what is ideally needed is a switchable mating
surface, where in one condition the surface has a high elastic
modulus and a very low coefficient of friction (similar to PTFE)
and in the other condition is extremely compliant and has a high
coefficient of friction (like silicone rubber).
In a real situation, the entire area of a compliant surface is
not in contact with the rigid surface over which it is intended to
propagate. The compliant mating surface contains a plurality of
approximately semi-spherical asperities, which may or may not
be in contact with the lower surface. This is illustrated in Figure
2.
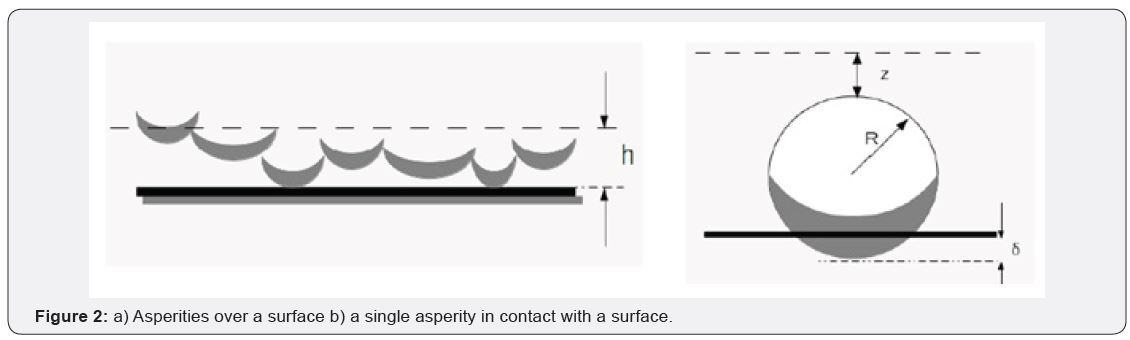
Given a nominal height between the two surfaces h, as shown
in Figure 2a, then only a small amount of asperity will be in direct
contact with the lower planar surface. Figure 2b illustrates the
situation for a single asperity with curvature radius R and
displacement z from the reference plane. At the point of contact,
the elastic asperity will deform with displacement [6].
Given a random variation in height h following a Gaussian
probability distribution, then the probability of contact is given
by (4).
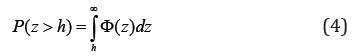
The number of contacts n can be calculated from the amount
of asperity N (5).

Using Hertz’s theory, the area of contact between the surface
and an asperity with displacement z is given by expression [7]
(6).
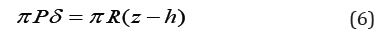
The area of contact (7) and the contact force {8} may be
calculated accordingly [6].

For the two mating surface materials, E1 and E2 are the elastic
moduli and υ1 and υ2 are the respective Poisson’s ratios.
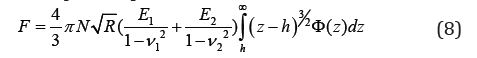
For an individual contact point, dividing (8) by (7), gives the
load pressure (9).
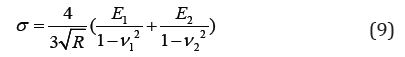
The greater the effective elastic modulus, the higher the
applicable load pressure. A lower elastic modulus results in
a correspondingly lower pressure for a given deformationcompliance.
When one of the surfaces is highly compliant, then
R also becomes a function of the applied pressure. Transposing
for R in (9) and differentiating gives (10).
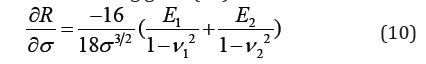
The function (10) tends to zero for large values of pressure,
thus making the effect stable. Furthermore, for a given surface,
either E1 or E2 will be rigid and constant. The
other must be
controllable in accordance with (3). Halling [3] also provides a similar
analysis for conical asperities but for the sake of brevity
this will not be included here [3].
Clearly, given a composite material with two sets of
controllable asperity, one with a high and one with a low frictional
coefficient, the criteria for a practical device laid out earlier, is
achievable. This principle already exists in nature. Eruciform
lifeforms employ soft prolegs with hard crochets on the ends to
allow switching between sliding and prehension. Although the
Gecko foot enjoys the ultimate natural prehension, it does not
adhere to a PTFE surface [8]. Furthermore, the objective in soft
robotics is to achieve this without resorting to direct methods of
mechanical alternation.
Magnetostiction
Here it must be distinguished between magneto adhesion
and magnetostiction. The former concerns simple magnetic
force produced when a magnetic field is applied against a
ferrous surface, while the latter relates to frictional changes
in the properties of a material caused by the application of
a magnetic field. When the coefficient of static friction s is a
function of an applied magnetic field, then the resulting force
which resists motion is the product of this frictional coefficient
m and the normal force FN. Magnetostiction should also not be
confused with magnetostriction. The latter refers to a second
order magneto-mechanical effect which leads to reversible
dimensional changes in specific magnetic materials [9].
Magnetoactive polymers (MAP) are polymer matrices containing
a dispersion of ferromagnetic or paramagnetic particles
distributed within a soft, nonmagnetic elastomer [10]. Their
mechanical [11] and electrical [12,13] properties have been extensively
investigated. Under the influence of a magnetic field
gradient, both magnetodeformation and an increase in elastic
modulus results [14]. Magnetodeformation can result in extremely
large displacements as is exploited in the design of origami
actuators [15].
If E1 or E2 in (9) is a function of the applied magnetic field, as
in the case of a magnetoactive polymer [14], then the criterion
outlined in (3) can be, at least partly, fulfilled. However, the
bulk permeability of a magnetoactive polymer changes with
mechanical deformation. This, in turn, changes the magnetic flux
density in the medium and with it the degree of deformation [16].
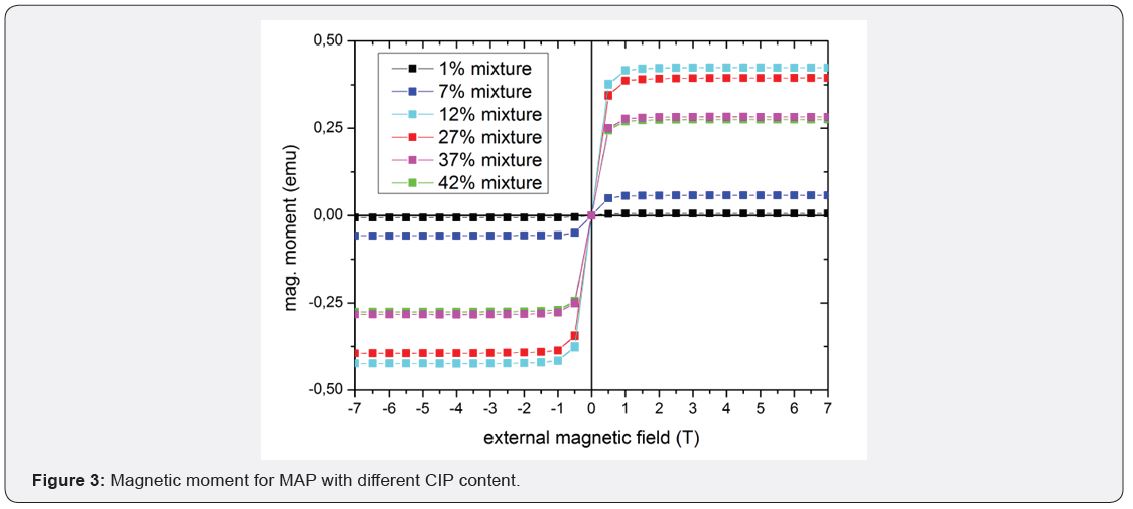
Magnetizations measurements carried out on 1mm³ samples
from the same production batch using a SQUID magnetometer
(Quantum Design MPMS XL) including MPMS RSO Controller
and digital R/G Bridge can be seen from Figure 3. Although
the maximum carbonyl iron powder (CIP) concentration does
not coincide with the maximum magnetization (which occurs
between 12%wt and 27%wt CIP), a compression of the MAP will
inevitably result in a localized increase in CIP.
The inclusion of hard magnetic particles allows the
MAP to
be permanently magnetized [17]. For example, Nd-Pr-Fe-Co-Zr-
Ti-Bm, SmCo or NdFeB are materials commonly used in modern
permanent magnets. Because of potential oxidation, the finished
magnets are usually chrome or epoxy resin coated. As well as
providing the elastic matrix, the polymer in a MAP serves the
same purpose. Unfortunately, this introduces a slight problem.
Profiling of a MAP surface alone rarely suffices as it is impossible
to use the magnetic particles themselves as asperities [18].
Inevitably in a MAP each magnetic particle is surrounded by
a thin layer of polymer, so the friction coefficient remains the
same with or without magnetic field. Magnetic particles not
completely surrounded by the polymer matrix rapidly detach
themselves from the matrix thus playing no further role in the
dynamics of the system. In addition, although immediately after
magnetization, each of the particles are magnetized in the same
direction, this situation rapidity changes as the magnetized
particles attempt to rotate within the polymer matrix in order to reach
the level of lowest energy [19]. This effect can be clearly
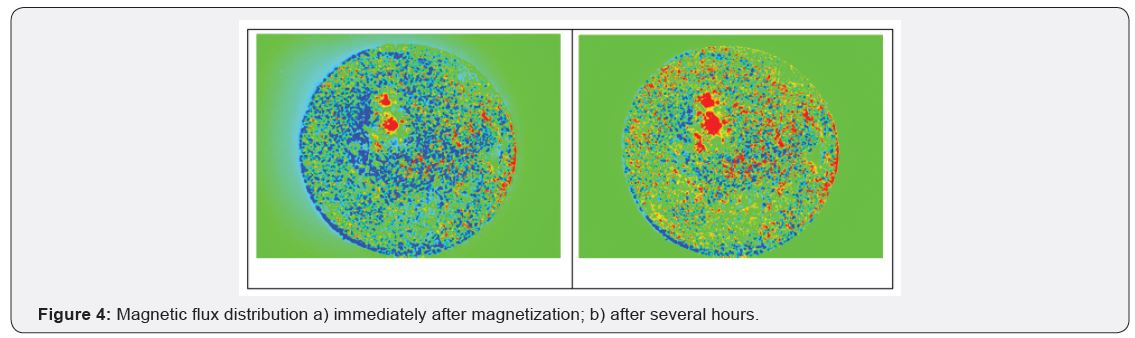
seen using a magnetic field camera (Matesy MagView) in Figure
4a which shows the magnetic flux density over the surface of a
hard-magnetic MAP immediately following magnetisation and
Figure 4b the same MAP several hours later where a substantial
portion of the particle orientation has changed.
In order to create an effective switchable stiction device with
two frictional states, two discrete areas of the same substrate
having different frictional coefficients must be presented.
A number of potential physical implementations exist, the
most effective of which are bistable devices [15] similar to the
previously mentioned insect prolegs. One portion of the device
comprises highly compliant addition-curing RTV-2 silicone
(Wacker Silicones) polydimethylsiloxane (PDMS) elastomer sans
magnetic content which exhibits a high coefficient of friction
between its under-surface and any surface in which it comes
into contact with. The other portion is magnetically active and
hardens under the influence of the magnetic field thus providing
a lower frictional coefficient and less compliance. This may also
be augmented by a metallic or PTFE layer to further reduce
friction.
The traditional means of ascertaining frictional coefficients
is the tilted plane method, where an object is placed on a sloped
surface and the slope angle gradually increased. Static friction
resistance develops when the object starts sliding [20]. At a
given time, the ratio between the load applied at right angles to
the sloped surface (W) and the friction resistance (F) is called
the coefficient of friction (f) and is determined according to the
following equation:
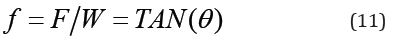
Much more accurate results may be obtained by measuring
the force threshold at the point of movement. Replacing FN with
mg in (1) and transposing for s gives (12).

Preliminary experiments were conducted on such a device
comprising two interspaced surface structures effectively
selectable by means of a magnetic field.
Experimental
A 6 axis Staübli RX60 [21] industrial robot equipped with
an ATI FTN-Mini40 6 d.o.f. force/torque sensor provided linear
movement of such a bistable element in both active and inactive
states [22]. Figure 5 shows the measured force in the Y-axis
(direction of movement) and the Z-axis (normal to the direction
of movement) for a linear displacement in the Y-direction.
Because compressive stress is by convention negative, the values
of force in the Z-axis of Figure 5 have been inverted.
The slight decrease in Fy at the beginning of movement is the
initial changeover from static to dynamic friction of the sliding
condition. The deliberate change from low to high friction
occurred at increment 4 along the abscissa of Figure 5.

Conclusion
Controllable stiction, as described in this paper, can be implemented
in many possible ways. The manipulation of mechanical
asperities on a surface can give rise to controllable friction.
However, this can only be achieved by the application of some
external influence such as an applied magnetic or electric field.
This paper has demonstrated how magnetostiction can be implemented
through magnetic field induced changes in the mechanical
properties, and in particular the elastic modulus, of
magnetoactive polymer substrates in order to control the friction between two surfaces. The application of magnetostiction
and its relevance to controllable motion in soft robotics has been
demonstrated as a practical example.
To Know More About Robotics & Automation Engineering Journal Please click on: https://juniperpublishers.com/cerj/index.php





No comments:
Post a Comment