Biostatistics and Biometrics Open Access Journal
Abstract
Rank-based method and least square approach are the
most common techniques for estimating the regression parameters of
accelerated failure time model. In this paper, both inference procedures
are considered, their advantages and disadvantages are explained, and
their similarities and differences are discussed.
Keywords:
Accelerated failure time model; Rank-based inference; Least square
method; Semiparametric method; Censored data; Linear regression;
Biostatistics
Introduction
Accelerated failure time model is an appealing
regression model to biostatistics researchers due to its simple
interpretation [1]. Estimating the regression parameters of the model
through parametric methods is quite challenging in the presence of
censored observations [2]. In such cases, semiparametric approaches are
very common. Two main semiparametric methods for estimating the unknown
parameters of the model are rank-based method [3], and least square
method [4]. In this paper, both inference procedures are briefly
explained and their main theoretical and computational aspects are
considered. Both approaches are also compared and their advantages and
disadvantages are discussed. The main focus of this study is on
investigating the similarities and differences of two methods in theory
as well as their performance in applications.
Inference procedures
Accelerated failure time model: For the ith subject of a random sample of n subjects let Ti denote the failure time, iC denote the censoring time, and Zi denote the 1p× vector of corresponding covariates. Assume that conditional on covariates ,Zi failure times Ti and censoring times Ci are independent. The accelerated failure time model takes the form
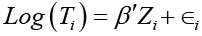
Where β is a p-vector of unknown model parameters,
and i∈ are the error terms of the model for 1,,in= with a common
distribution function F which is unspecified [5]. The
data consists of 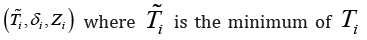 and
and 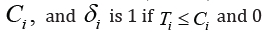 otherwise. The introduced model is a semiparametric linear regression
model which relates the log-transformed failure times to the covariates.
otherwise. The introduced model is a semiparametric linear regression
model which relates the log-transformed failure times to the covariates.
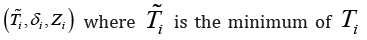 and
and 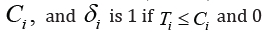 otherwise. The introduced model is a semiparametric linear regression
model which relates the log-transformed failure times to the covariates.
otherwise. The introduced model is a semiparametric linear regression
model which relates the log-transformed failure times to the covariates.Rank estimators
Define 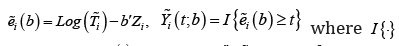 is the indicator function, and
is the indicator function, and 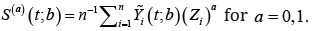 The weighted log-rank estimating function for the unknown parameter β is given by
The weighted log-rank estimating function for the unknown parameter β is given by
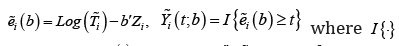 is the indicator function, and
is the indicator function, and 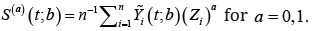 The weighted log-rank estimating function for the unknown parameter β is given by
The weighted log-rank estimating function for the unknown parameter β is given by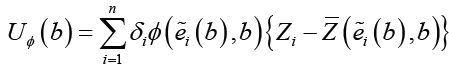
Where 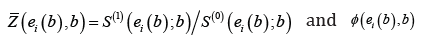 is a weight function. The estimating function correspond to Gehan
is a weight function. The estimating function correspond to Gehan 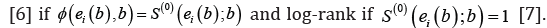 Let ˆRβ denote the rank estimator for the unknown parameter of the
model which is the solution of (){}0.Ubφ= For estimating the unknown
parameters of the model Jin et al. [3] proposed an iterative algorithm
on the basis of the general weighted estimating function. The algorithm
at its kth iteration is given by
Let ˆRβ denote the rank estimator for the unknown parameter of the
model which is the solution of (){}0.Ubφ= For estimating the unknown
parameters of the model Jin et al. [3] proposed an iterative algorithm
on the basis of the general weighted estimating function. The algorithm
at its kth iteration is given by
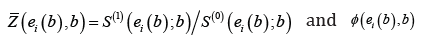 is a weight function. The estimating function correspond to Gehan
is a weight function. The estimating function correspond to Gehan 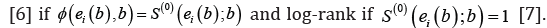 Let ˆRβ denote the rank estimator for the unknown parameter of the
model which is the solution of (){}0.Ubφ= For estimating the unknown
parameters of the model Jin et al. [3] proposed an iterative algorithm
on the basis of the general weighted estimating function. The algorithm
at its kth iteration is given by
Let ˆRβ denote the rank estimator for the unknown parameter of the
model which is the solution of (){}0.Ubφ= For estimating the unknown
parameters of the model Jin et al. [3] proposed an iterative algorithm
on the basis of the general weighted estimating function. The algorithm
at its kth iteration is given by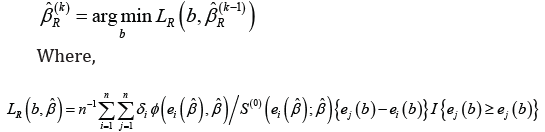
According to Jin et al. [3] the rank estimator 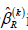 is asymptotically normal for any .k
is asymptotically normal for any .k
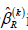 is asymptotically normal for any .k
is asymptotically normal for any .k Least square estimators
When there is no censored observations the least
square estimator of the unknown model parameters is obtained by solving
the following estimating equation:
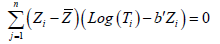
This estimating equation cannot be used when data
contains censored observations since the actual value of iT is unknown
for subject i when 0.iδ= For obtaining the least square estimators in
the presence of censored data Jin et al. [4] proposed an iterative
algorithm which at its kth iteration is given by
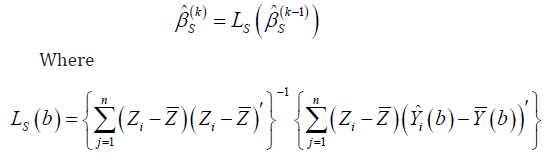
In this equation,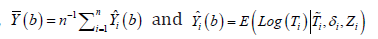 which is proposed by Buckley & James [8] and can be approximated by
which is proposed by Buckley & James [8] and can be approximated by
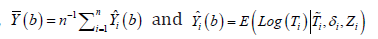 which is proposed by Buckley & James [8] and can be approximated by
which is proposed by Buckley & James [8] and can be approximated by 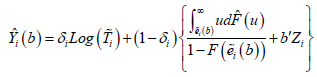
Where ˆF is the Kaplan–Meier estimator of .F
According to Jin et al. [4] the least square estimator ()ˆkSβ is
asymptotically normal if the initial value ()0ˆSβ is asymptotically
normal.
Discussion
Both the rank-based method and the least square
approach are semiparametric inference procedures since the probability
distribution of error terms of the model is completely unknown. One
advantage of rank-based inference over the least square method is that
it does not involve estimating the distribution of the error terms,
while obtaining least square estimators requires the Kaplan–Meier
estimator of the distribution of the error terms. This makes the least
square method and its corresponding algorithm more complicated than the
rank-based method, both theoretically and computationally. Note that,
both algorithms need a consistent estimator of the model parameter such
as Gehan estimator for their initial values. Thus, the least square
approach requires to obtain a rank estimator prior to the computational
stage of its associated algorithm. In addition, it has been established
that rank estimators are always asymptotically normal [9,10] while the
asymptotic normality of least square estimators strongly depend on the
asymptotic normality of the initial value of their corresponding
algorithm. However, the results of the simulation studies by Jin et al.
[4] illustrated that there was no significant difference between the
efficiency of rank estimators and least square estimators. More
precisely, the rank estimators were slightly more efficient under
extreme-value error, and the least square estimators were slightly more
efficient under logistic and normal errors.
Conclusion
For estimating the regression parameters of
semiparametric accelerated failure time model both rank estimators and
least square estimators are common. From a theoretical point of view,
rank-based inference procedure involves less technical difficulties
since it does not require estimating the probability distribution of the
error terms while least square approach involves Kaplan–Meier estimator
of the distribution of the error terms. Moreover, the asymptotic
normality of rank estimators does not depend on the distribution of the
initial value of its associated algorithm. In application, the results
of simulation studies show that there is no significant difference
between the efficiency of rank estimators and least square estimators.
Therefore, in studies that researcher is free to choose between these
two methods rank estimators are definitely more recommended than least
square estimators.
To Know More About Biostatistics and Biometrics Open Access Journal Please click on:





No comments:
Post a Comment