Journal of clinical and medical imaging Juniper Publishers
Authored by Bassey E
Abstract
Informed by the lack of definite approach for parametric estimation for the dynamics of dual infectious diseases, this article articulates a basic five-dimensional (5D) - mathematical model. Formulation of the model is presented as a problem of optimization control dynamics of Pathogen-Induced HIV infections. Used as a therapeutic treatment - reverse transcriptase inhibitor, the study aimed at maximizing target functional based control system; that is, to maximize the total number of CD4+ T-cells and minimize the cost of treatment (RTI). Transformation of the model was carried out using ordinary differential equations and analysis performed by a numerical method solved on the basis of a special discretization method called AVK method. The model further resorted to a series of numerical illustrations simulated by a known Runge-Kutter of order of precision 4 in a Mathcad environment. Results of analysis indicated that for defined control function and consistent optimal control therapy given at a steady systemic cost, maximization of healthy CD4+ T cells concentration was assiduously achieved within time interval of 18 years, under a realistic optimal control therapeutic treatment. The study therefore, recommends as a basis, the use of this model in optimization problems of other infectious diseases.
Keywords: optimization; viral-load; pathogen; discretization; therapeutic; treatment; maximization; minimization; replication; estimation; asymptomatic
Background
Of utmost concern to the scientist, is the lack clear indication for proper documentation of cogent cures for the dreaded human immune deficiency virus (HIV), which usually metamorphoses into acquired immune deficiency syndrome (AIDS). Therefore, continuous research work predominantly on the suppression and prevention of the disease remains an area of paramount interest. Furthermore, the multiplicities of diverse new cases of HIV/AIDS have in no small measure put researchers under an intense pressure. Instances abound where patients are infected with more than a single virus (i.e. HIV with tuberculosis; HIV with hepatitis C; HIV with parasitoid-pathogen, etc.).
Formulation and analysis of the mentioned cases involves a number of parameters. Yet, not much or very little attention has been focus on the estimation of these parameters [1]. Exceptional works on this direction include only on virus clearance rate and the death rate of infected CD4+ T cells [2,3]; the analysis based on the quasi-steady state of the asymptomatic period before it is disturbed by chemotherapy [4]. In [1,5,6], attempts were made on the estimation of parameters of single virus infection-HlV. The model [2,7], discussed the infectious disease at the cellular level to describe the immune system and the host-pathogen interaction.
ln this present paper, we consider the multiplicity situation with particular attention on HlV-infection induced by parasitoid- pathogen. Here, we formulate a mathematical model which studies the parametric estimation of dual infection (viral load and pathogen), as against several works on single infection [1,2,5-7]. The population density, with which the model is formulated, consists of 5 different subgroups, giving rise to basic 5- dimensional (5D) ordinary differential equations, presented as an optimization control problem. The model is subjected to reverse transcriptase inhibitor (RTI), as a therapeutic factor with the aim of minimizing the systemic cost of treatment.
The objective of optimizing the model is the affordability of predicting infection early stage-called 'set point”, a vital breakthrough in treatment decision making [1,5]. Therefore, the present work does not only account for the estimation of all parameters in the dynamics of the dual infection, but also account for viral load replication and pathogen resistivity.
The model explores a well-known numerical method-the discretization method called A.V. Kamyad method in solving the formulated 5D- optimal control model with numerical illustrations using Runge-Kutter of order 4 in a Mathcad environment. Basic 3D models have been formulated [3,6].
Other notable models involving discretization method in the optimization control of parameters for single infection includes [7-9]. The deployment of highly anti-retroviral therapy (HAART) regimen on treatment and suppression of viral replication and immune system recovery can be found in [6,10,11]. The models [12,13], treated optimal control of HIV infection using Boubakar polynomials expansion scheme and Fuzzy dynamical system respectively. The paper [14], had discussed the impact of numerical stability of the treatment of vertical transmitted HIV/AIDS infections; while Global Convergence and Impact of Multistage and Pade Techniques for Iterative Methods in Nonlinear HIV/AIDS Preventive Chain Model can be found in [15]. The existence and uniqueness of optimal control pair for treatments of an HIV immunology model was studied [16].
The entire model is composed of the introductory aspect as section 1. Definition of the model problem statement and mathematical formulation are absorbed in section 2. Section 3, is devoted to the method and parameter estimation of the model, which explored the AVK discretization methodfor the analysis of the optimal control strategy.Numerical simulations of model illustrations and discussion were designated for section 4. Finally, in section 5, we summarized the work, following the observatory conclusion and remarks base on the formulation and extensive analysis of the model. It is hope that from our present 5D-model, more insight into the optimality of parameter estimation for dual infectious diseases using AVK method of discretizationwill be uncover.
Problem Statement and Model Formulation
In formulating this model, we shall bring to fore, relating ideas of ordinary differential equation in mathematical modeling, structured as problem statement of optimization control, which are solvable using well known method from numerical methods.
We construct our model from a considered population density consisting of five different subpopulations giving rise to a set of five ordinary differential equations. Physiologically, let Tu denote the uninfected CD4+ T cells, Vv - HIV virus (viral load), Pp - parasitoid-pathogen; then for virus-infected CD4+ T cells , we shall denote by I(v)andI(p) respectively. The biological descriptionsof the parameters with which these variables interact are are defined by [17] and its corresponding ODE's are derived as:
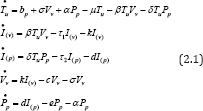
Biologically, equation (2.1) assumed a relatively steady viral level during the asymptotic stage of HIV and pathogen infection known as “set-point”. At this initial set-point, the body develops an immune system called, the innate immune system, which act as antibodies against HIV-infection and pathogen barrier preventing mechanism. However, the replication of viral load and the rapid adaptivity of pathogen make it impossible for easy detection and neutralization by this innate immune system and gradually leading to full blown AIDS [1, 18,19].
Furthermore, it can be shown mathematically from equation (2.1), that the amount of and in the set-point are given by the equilibrium of virus and parasitoid-pathogen depicted i.e.
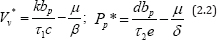
Thus, model (2.1) adequately reflected the disease progression from initial infection to an asymptotic stage [6].
Methods and Parameter Estimation
In this section, we outline our choice method-the discretization method, which is aimed at estimating all the parameters of HIV and pathogen as involved in our basic model (2.1). This is followed by the optimization control of the uninfected CD4+ T cells and minimizing the cost of treatment factor
Discretization of the Model
Discretization method affords us the opportunity to transform equation as in model (2.1) into solvable discrete form. Clearly, with discretization method, all the twelve parameters in model (2.1) can be estimated (or measured). As a limitation, we shall deliberately omit the variables Iv andI(p) in the initial process due to higher cost quantification of these infected cells [1]. The emphatic nature of this limitation is also stress by [5], on the ground that, the number of infected CD4+ T cells is found to be too small compared to the number of healthy CD4+T cells.
Now, let y1 = Tu , y2 = Vv, andy3 = Pp . Then, the higher order differential equations of the output can be derived as:
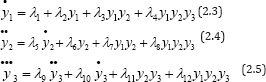
Where
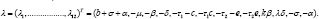
We λ , as invertible i.e. having a one-to-one mapping for β ≠0,δ ≠ 0 andτi,2≠ 0 . Therefore, the identification of the original parameters of model (2.1) is equivalent to identification of λ . It is known that for most HIV patients, β ≠ 0 and τ1 < c , which also holds for δ ≠ 0 and τ2< e [5]. Then, the following inverse map can be derived as:

Now, observing equations (2.3)-(2.5), we see that each of them contains four parameters, therefore, it is necessary to further generate at least three other equations on the bases of each of them. This is achieved by differentiating equations (2.3)-(2.5) more times in order to produce the upper derivatives of , y1, y2. y3 Then, it becomes obvious that at least, four measurement of y1 , CD4+ T cell count, five measurement of y2 , viral load and six measurement of y3 pathogens are needed for a complete determination of equation model (2.1) parameters [5].
As a lid way, we assume that the following measurements are available:
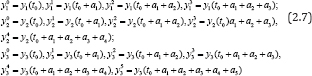
Then, by discretization of equations (2.3)-(2.5) and substitution of approximate values of the first derivative of y1 , the first and second derivatives of y2 ; and the first to third derivatives of y3 for CD4+ T cells, viral load and pathogen respectively, we can establish the measurement of the variables at different time intervals i.e.
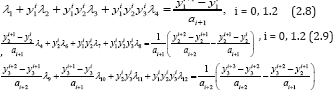

So, we could as well obtain similar matrices for equations (2.9)-(2.l0). Thus, the variables λi., i = 1, 2... 12 and all the parameters from equation (2.6) of the basic model, can be calculated. A case study of some of the parameter estimation as in basic model (2.1) can be found in [5]. Now, applying the bases of equation (2.7), we establish (Table 1) below, the available measurement for the count of CD4+ T cells, viral load and pathogens at varying time intervals:
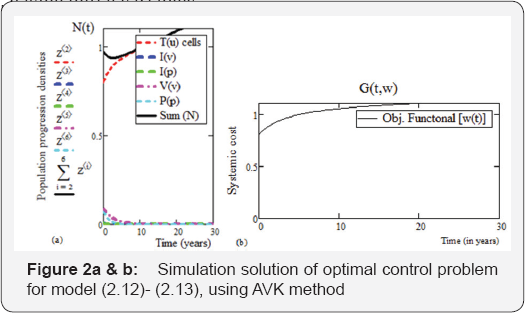
Therefore, the solution of the model (2.1) for t ∈[0,30] with the initial values defined i.e. T0(u) = 0.6,I0(v) = 0 ,I0(P) = 0 , V0(v) = 0.2 andP0(P)= 0 2 is determined using well-known numerical method like RK4 in a Mathcad environment.The graphs simulation of the susceptible CD4+ T cells, virus -infected CD4+ T cells, viral lead, pathogenic-infected CD4+ T cells and the parasitoid-pathogen, will be presented in section four.
Optimal Control of HIV and Pathogen Infection
The increasing therapeutic drugs for the treatment of AIDS which also serve as treatment of most pathogens by the activation of required immune system (adaptive immune system) can be conveniently grouped into three major groupsReverse transcriptase inhibitor (RTI), protease and integrase enzyme inhibitor. In this present model, we conduct our studies using the (RTI). This choice for RTI is not unconnected with the dual characteristics of RTI on both viral load and the activation of adaptive immune system against parasitoid-pathogen. RTI is responsible for the prevention of uninfected lymphocyte cells from infection by viral load and as well elimination of infected pathogen cell [16]. Corroborating the above assertion is the commensurate reaction of these two infectors with their host as reference in Table 1:
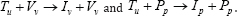
Therefore, the utmost concern of the present work is to control model (2.1), in order to prevent any transmission of uninfected cells to virus and pathogenic infected cells. This control function is given as w(t) , where 0 ≤ w(t) ≤ 1 .The most efficiency ofdrug in this case, is when , implying that CD4+ T cells are not infected by viral load and pathogen anymore. At the tail side, if , w(t) ≡ 0 then drug is said to be inefficacious and therefore, disease progression does not change. On the basis of this constrains, we derive from model (2.1), the control system as follows:
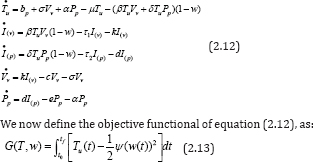
using [19], with the weight factor ψ = 10. Here, we aimed at maximizing the objective functional (2.13) subject to the control system (2.12); that is, maximizing the total count of CD4+ T cells and minimizing the cost of treatment via RTI drugs. We resolve this optimal control problem by numerical methods [7], using a special discretization method called A.V. Kamyad [19,21]. Applying the AVK method, we let,

Step2.Combining the total error function with the objective functional (2.14), we have,
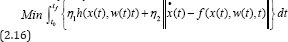
Subject to: x(t0)=x0,x(tf)
where η1 , η2 are two weighted positive integers, given thatη1+η2=1 .
Step 3.Induce error control measure called the constraint to the error, i.e. E1 (x,w) ≤ ε ,
to the optimal control problem in step 2. Therefore, the modified optimal problem arising from equations (2.14)-(2.15), is reformulated as:
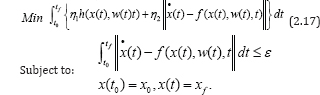
Step 4.Calculate w(ti) by minimizing the optimal control problem (2.17), using discretization method. Let the norm function be given as norm 1, and then we can solve the optimization problem that follows:
be given as norm 1, and then we can solve the optimization problem that follows:
 be given as norm 1, and then we can solve the optimization problem that follows:
be given as norm 1, and then we can solve the optimization problem that follows:
Step 5.Taking from w(tt), for every as in equation (2.15), it is clearly seen that we can find , x(ti) for any . i = 0,1, , r -1
We then apply this technique to calculate the control problem of equation (2.12), with the objective functional (2.13). The parameters used in the basic control model (2.12) are in agreement with that in [5]. So, we can assume that the treatment starts when CD4+ T cells was at minimum count as pathogen is on the decrease. Results are then confirmed by extrapolation from our treatment intervals. Therefore, from Figure 1, for T (3) = 0.8 , is said to be minimum count of CD4+ T cells. This shows that treatment interval is [3,30] years. Furthermore, we finally partition [3,30] years into r parts with length g. Thus, the discretization of equation (2.18) becomes:
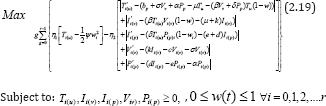
and taking its initial values of the variables from the results of the basic model (2.1), where, 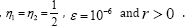 .
.
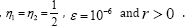 .
.
We present numerical illustration and results of this optimization problem which is obtained using RK4 in a Mathcad environment in the coming section.
Numerical Results and Discussion
Using an optimal weight factor ψ = 10 , numerical solutions for the uninfected CD4+ T cells, viral load, and pathogen concentration, as well as the optimal treatment strategy have een generated. From Figure 2 below,the solution fortε[3.30] having initial variable
T0(u) = 0.6,I0(v) = 0,I0( p) = 0,V0(v) = 0.2, P0( p) = 0.2,and parameter values as in Table 2 below:is used for the determination of treatment “set point” and the concentration of various population density understudies. It is seen from the graphical representation that at T (3) = 0.8, is the minimum count of CD4+ T cells. So, the treatment interval is[3,30] years. Noted that this interval includes: .
I(v) = 0.01,I( p) = 0.01, V(v) = 0.08, P( p) = 0.07

This result forms the led way for the determination of the optimal control of uninfected CD4+ T cells and minimization of therapeutic treatment via the discretization techniques called the A.V. Kamyad method. From Figure 2a & 2b below, the solution fort ∈ [3.30] , having initial variables , T0(U) = 0.8,I0(V)0.01,I0(P) =0.01,V0(v)) = 0.08, P0(p) = 0.07 with parameters values as in Table 3(a) below: represents the calculation for the maximization of the uninfected CD4+ T cells while minimizing the systemic cost of therapeutic treatment (RTI). We observed that from Figure 2(a) below, with control function w(t) = 0.5, infection is near eradication at an early period of 4 years for pathogen and 10 years for viral load i.e. Tu (10) = 0.94 , Iv = (10) = 0 ,Ip = 0 , Vv(10) = 0.02 , Pp(10) = 0.01 . The concentration of the uninfected CD4+ T cells is seen increasing rapidly, which affirmed the overall healthy population density. From Table 3(b) below, as illustrated by Figure 2(b) above, we see that as optimal therapeutic treatment is consistently given at a steady systemic cost, the uninfected CD4+ T cells increases in a logistic way (manner), explaining why in Figure 2(a), the viral load and pathogen decreases in concentration in the blood plasma. Figure 2(b) shows that active therapeutic treatment terminates after 18 years, which again ascertained the necessity for our initial pre-condition for a definite time interval for a realistic therapeutic investigation.

Mathematically, from the state system (2.12)-(2.13), the choice for the time interval t ε [3,30] conveniently accommodated the clinical latency stage, which has a maximum period of 10 years [22]. Moreover, the weight factor ψ, determined the level at which therapeutic treatment is administered within the period of time. The implication is that if systemic cost of treatment increases, the patient receives the maximal therapy for a finite period of ψ factor,

Conclusion
In this paper, numerical optimization of nonlinear 5-Dimensional mathematical HIV dynamic model for the parametric estimation of pathogenic induced HIV infections was formulated. The dynamics of the infection was presented as optimization control problem, solvable by a special discretization method called AVK method. Numerical computations showed that, with defined control function, a realistic optimal control minimal therapeutic cost can be achieved within measured time interval of 18 years, while assiduously maximizing healthy CD4+ T cells concentration as a measure of the parameter estimation. The study therefore, suggests the use of the model for the optimization control problems of other related infectious diseases.
To Know More About Journal of clinical and
medical imaging Please Click on:
https://juniperpublishers.com/ctcmi/index.php




No comments:
Post a Comment