Oceanography & Fisheries Open Access Journal - Juniper Publishers
Abstract
In this paper, the general behaviour of the marine circulation (sea currents) and the resulting patterns caused by wind action in the central part of the South Euboean Gulf is studied using a three-dimensional hydrodynamic model (ELCOM). The work was part of a study effort to exploit the fresh water jets that spring from the bottom of the sea, off the port of Eretria (these underwater karstic springs in the sea are called anavalos in Greek). The specific objectives were to determine the shape of the depth-averaged currents resulting from typical wind conditions and to estimate the typical time of adaptation of currents to changes in wind conditions. The South Euboean Gulf is a relatively narrow strait formed between Attica and the southernmost part of the NE coast of Central Greece, with only its central part having a considerable width, and extends for about 55 nautical miles from southeast to northwest. For the bathymetry a variable grid was used and the model was put to run simulations for each of the eight primary wind directions, for a time period of three consecutive days and then pause abruptly. The simulation period extended to seven days so as to consider the times of adaptation. No stratification was considered. The results seem very plausible and indeed are confirmed by dimensional analysis that is included in this paper as an appendix.
Keywords: Wind induced sea currents; South Euboean Gulf; Greece; ELCOM model
Introduction
The Euboean Gulf has been a subject of scientific inquiry from the days of the ancients Greeks, due to the very strong tidal effect that characterizes the strait of Euripus, near the city of Chalkis. The strait is subject to strong tidal currents which reverse direction approximately four times a day. Although tidal flows are very weak in the Eastern Mediterranean, this strait is an exception. Amongst the early scholars who studied the phenomenon we find Eratosthenes, Pitheas, Posidonios, Stravon and Senekas. There is even a tradition that Aristotle committed suicide by falling into the waters of Euripus, because he could not solve the problem, saying the famous "Since thou did not send Euripon to Aristotle, thou sent Aristotle to Euripus". This is a myth of course, because Aristotle died in Chalkis, but he died a natural death. The Gulf has been the subject of a number of studies also from the early 20th century. Forel, the ‘father’ of Limnology, was one of the first to suggest an explanation, but a more complete analysis was presented by Aiginitis, director of the Athens Observatory, who published his conclusions in 1929.
The shape of the Gulf, and especially its southern part, south of Chalkis, being effectively an enclosed sea water body with very specific boundary conditions to its Northern end, lends itself to hydrodynamic modelling. The first hydrodynamic model for the whole of the Gulf (both its Northern and its Southern part) was constructed by Livieratos, while Tsimplis applied two models, a low resolution one for the propagation of tidal waves in the northern and southern Euboean Gulf and a high resolution one, focused on the Gulf’s Straits. Tsirogiannis et al. simulated the whole of the Euboean Gulf using the ELCOM model with important findings [1].
It is important to understand the physical processes and mean circulation patterns since they provide an indication of transport pathways of nutrients, contaminants and sediment (suspended particles). To this end, 3‐D coastal ocean models have been developed by various researchers and Universities, like for instance Princeton Ocean Model (POM), which is considered one of the first. One such model is ELCOM that solves the hydrodynamic and the continuity equations assuming hydrostatic conditions and the Boussinesq assumptions. ELCOM (Estuary, Lake and Coastal Ocean Model) [2] has been developed by CRW (Center for Water Research, University of Western Australia), and has been used extensively over the last 15 years in simulating marine and coastal ocean environments, lakes [3-5], river plume dynamics [6] and even stabilization ponds systems [7]. Modeled and simulated processes include baroclinic and barotropic responses, rotational effects, tidal forcing, wind stress, surface thermal forcing, inflows, outflows, and transport of salt, heat and passive scalars [7]. It is worth noting that ELCOM usually requires minor calibration adjustments, since the variation of most of its parameters is well defined by the conservation equations of mass, momentum and energy containing few adjustable coefficients, unlike its coupled model CAEDYM, dedicated to water quality simulation, that appears more sensitive to field data [5].
This study can be thought of as a numerical experiment or investigation, in the sense that no measured/observed field data were used for the simulations or the validation. The meteorological forcing was represented by a seasonal average for the seven days that each of the eight simulations was performed-one for every wind direction. The purpose was to determine the shape and magnitude not only of the surface currents, but also the bottom and depth-averaged circulation resulting from typical wind conditions.
Materials and Methods
Study Area
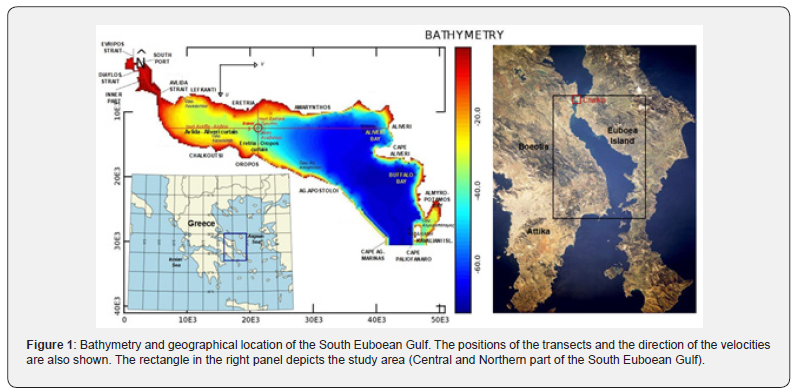
The South Euboean Gulf is formed between the eastern coast of Attica (southwards) and the southernmost part of the NE coast of Central Greece (northwards) which form its south-western shores and the southernmost part of the SW coast of the island of Evia which form its NW shores. This rather narrow and elongated sea area extends for about 55 nautical miles from southeast to northwest and is divided into three distinct parts: The Gulf of Petalia or outer part, the central part and the innermost point of South Euboean which in turn consists of the inner (northwest) part, the Strait of Diaylos and the South Port of Chalkida [8].
The central part of the South Euboean Gulf (Figure 1), which is the study area, has the southeastern boundary of Akra (=cape) Paliofanaro of the Kavalliani Island, the southwestern boundary of Akra Agia Marina and the northwestern boundary of Akra Avlidos, about 24 miles northwest of Akra Agia Marina, while the northeastern boundary is Akra Bourtzi, which is located at the same distance northwest of Akra Paliofanaro. This section extends for about 25 miles (46.3 km) from SE to NW and its width, around its middle, is 8 miles (14.8 km). The southern entrance (Kavaliani) of the central part is 1.4 miles (2.59 km) wide, while the northern entrance (Avlida) is 3/10 of a mile (0.55 km) wide and is the narrowest point of the strait of the same name (Avlida-Bourtzi). The extent of the sea area of the central part is about 460 km2 and the perimeter is roughly 160 km.
The sea depths at the southern entrance are about 70m in the middle of the distance between Isl. Kavaliani and Akra Agia Marina, while along the axis of the Avlida Strait the depths range from 8 to 14 m. The bathymetry of the bay reveals the existence of a steep slope in the direction west to east where a difference in depth of about 25 m is observed over a length of about 10 km (from the middle of the distance between Eretria and Amarynthos to the coast of Amarynthos). This slope can be said to divide the bay into a deep eastern part (east of Amarynthos) with an average depth of 53m, and a shallow western part (west of Eretria) with an average depth of 23m. The depths in the cove (inner part and South Port of Chalkis) are much shallower with a maximum depth of 10 m.
The prevailing winds according to the wind data of the Chalkida meteorological station are the North (23.4%), the Northeast (21.7%) and the Northwest (17.9%). The other winds occur with relatively low frequency (5÷7%), except for the West winds which occur relatively more frequently than the others (8.1%) [8]. Cloudiness occurs 5% of the time
ELCOM model and set-up
For the numerical simulation, as earlier mentioned, the ELCOM (Estuary, Lake and Coastal Ocean Model) model was used, a 3D finite-difference model suitable for simulations in lakes and enclosed water bodies. The main equations are the Reynolds averaged Navier-Stokes (RANS) equations using the Coriolis term, following the Boussinesq approximation and ignoring non-hydrostatic pressure terms. For the turbulence, as far as the horizontal is concerned, a constant eddy viscosity coefficient is used, while for the vertical the coefficient is obtained as a function of a local Richardson number. The density is calculated as a function of temperature and salinity according to the UNESCO equation [2].
The bathymetry was derived from digitizing the map of the Hydrographic Service of the Navy. The horizontal resolution was 200x200 m in the largest part of the field, while in parts of the field cells of other dimensions were used (non-uniform grid) in order to represent dimensions smaller than 200 m (such as the Euripus Strait). The total number of surface cells was 11,565. The following surface-to-bottom resolution was used for the vertical: 0.5 +0.5 +0.7 +0.8 +1.3 +1.7 +2 +2.5 +2.5 +2.5 +5 +7 +8 +10 +10 +10 +10 = 75m. The total number of computational cells was 162,565. A constant and uniform sea temperature of 17ºC (late autumn - spring), and a constant wind speed of 7 m s-1 (4 Beufort) was assumed. In the northern and southern boundaries of the computational domain, an “open” boundary condition was applied, which passively allowed the water inflow to, or outflow from each cell, according to the corresponding flow needs.
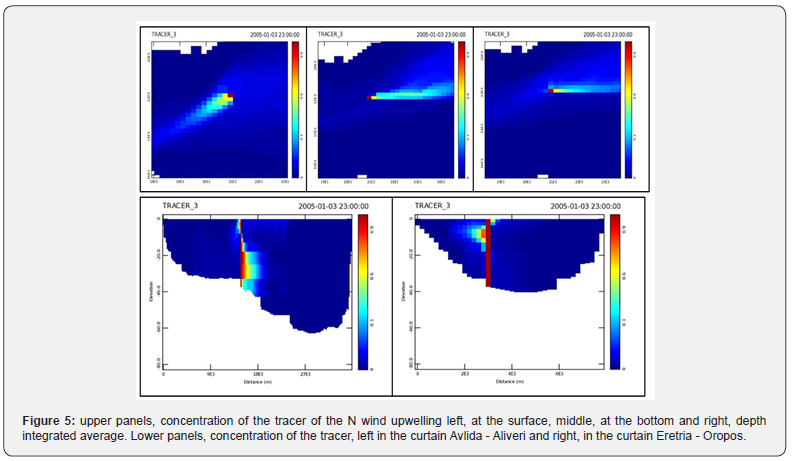
The time step was 30 sec. and the duration of the simulation was 7 days for each of the eight winds. The wind blew continuously for the first 3 days and stopped abruptly at the beginning of the fourth day. Both the dimensional analysis and the results of the simulations showed that this time period was sufficient for the flows to stabilize at the end of the third day (in fact in a much shorter time). The inertial oscillations that followed the wind cessation, however, generally did not seem to fully damp out over the next 4 days. For the visualization of the results, the model allows the creation of “curtains” i.e. sections of the water body along given lines, as well as three types of plan views or “sheets”: the surface layer (top), the bottom layer (bottom) and finally the average layer (average), which is the depth-integrated result of the parameter of interest. We used two perpendicular 'curtains' (Figure 1) at the intersection of which the position of the Eretria’s anavalos is roughly located. These curtains are a) Eretria - Oropos and b) Avlida - Aliveri. It should be emphasized here, for the sake of understanding the diagrams that follow, that the speed U increases downwards, while the speed V increases to the right. Thus, V is perpendicular to the curtain of Eretria (with positive values meaning flow towards Aliveri), while U is perpendicular to the curtain of Avlida (with positive values meaning flow towards Oropos). Finally, a tracer (Tracer_3, Figure 1) at the intersection of the two curtains was used to visualize circulation at this location.
Results
Below we will describe the actual three-dimensional circulation patterns resulting from the wind blowing for a long time from a given direction. We are going to consider winds in pairs in order to avoid confusion from the many cases.
North - Northeastern wind
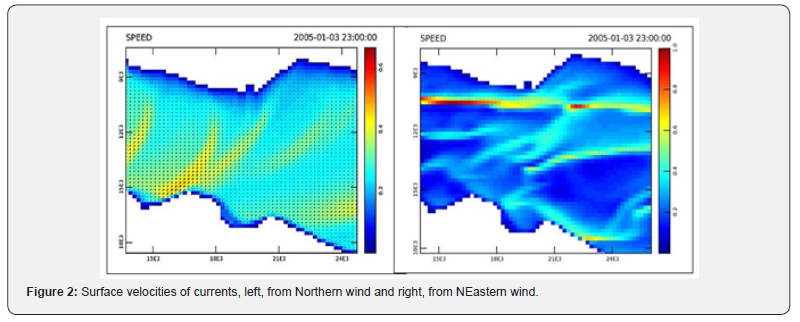
On the surface, the Northern wind breeze causes 'gusts', i.e. areas of confluence of relatively strong currents in a SW direction, while offshore, i.e. towards the Gulf of Aliveri, they take a more Western direction, as the Figure 2 shows. The northeast wind blast causes stronger currents with a westerly direction. A strong 'gust' passes off Eretria, with speeds up to 1m/s. However, it should be mentioned that of the 8 winds simulated, NE appeared unstable, i.e. the equilibrium state at the end of the adjustment time was not evident.
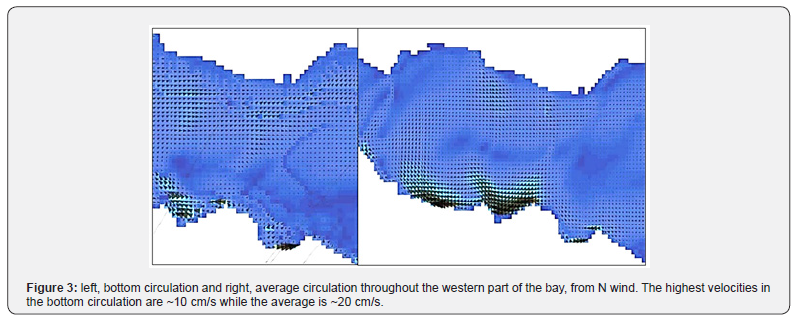
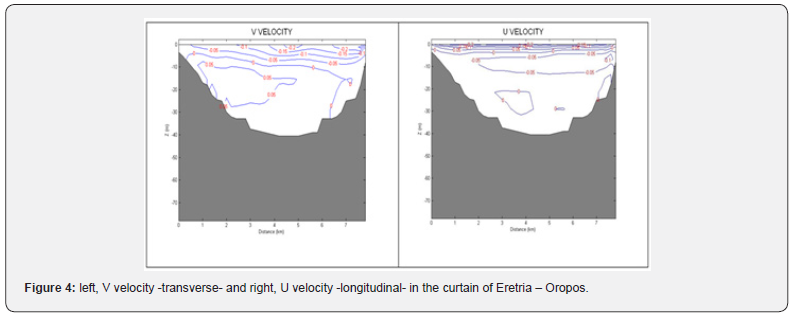
The circulation on the seabed created by the Northern wind is generally directed E and NE except for the bay of Chalkoutsi where the seabed flows 'turn' to NW (Figure 3). The resulting average circulation, as shown in Figure 3, is a cyclonic gyre with higher average speeds on the southern coast (Oropos and Chalkoutsi). We can observe this pattern also in the Eretria curtain with lines of equal V velocities in Figure 4.
As one can see in Figure 4, the transport to Avlida takes place on the surface, while deeper there is transport to Oropos. Positive velocities - towards Aliveri - are found throughout the central part at depths below 10 m and mainly in the deeper parts of Eretria. Velocities here reach and exceed 5 cm/s. Figure 4 on the right is more difficult to read as the U velocity is parallel to the axis of the plot. However, a surface layer of about 5 m thickness with transport towards the Oropos and velocities at the surface of ~20 cm/s is shown here, while deeper in the Oropos a return current with velocities of ~5 cm/s is shown which occurs at a depth of 6 to 13 m. The total transport that takes place in the region can also be visualized using the tracer, and is shown in Figure 5. As we can see, the current generated at the surface is 45 degrees to the right of the wind, while at the bottom it is 90 degrees to the left. The average transport is almost similar to the bottom transport indicating that the main transport occurs with the bottom Ekman layer rather than the surface layer. The shape of the spiral is shown in Figure 5 below which is the Avlida-Aliveri curtain.
Western – Northwestern wind
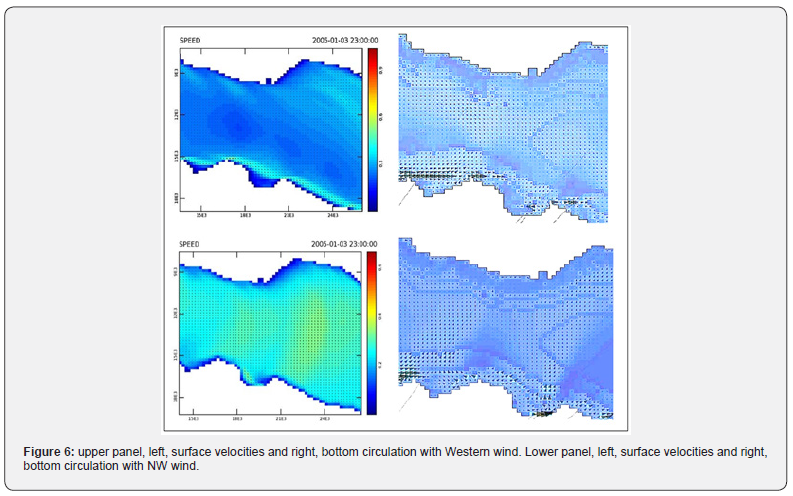
On the surface, the westerly wind creates strong surface currents along the southern coasts (Dilesi - Chalkoutsi - Oropos - Ag. Marina). The NW wind breeze creates a nearly homogeneous surface velocity field with a N to S direction (Figure 6).
On the bottom, with a westerly wind, we have a reverse flow to the W and NW in the centre of the bay and near Eretria, while on the southern coast we have the same flow as the surface flow. The average transport occurs on the North and South coasts towards E and SE with a small return flow in the centre of the bay. Overtopping is observed on the W oriented coasts. With a NW wind, the velocities in the bottom layer shift to the north. The free surface level is lowered in the interior of the bay. The surface speed of the current is at 45 degrees to the right of the wind. The bottom velocity as well as the average is again at 90 degrees to the left of the wind.
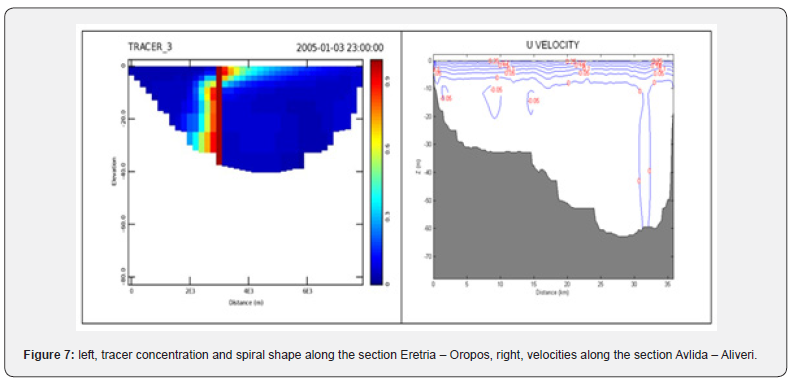
The NW wind circulation on the surface is therefore towards Oropos, while in deeper parts of the bay is towards Eretria. This is illustrated in Figure 7 where in the surface layer of about 10 m thickness the transport is towards Oropos, while below this depth there is a weak flow in the opposite direction, with higher velocities ~5cm/s, in the layer from 10 to 20 m depth, and mainly within the shallow part of the bay.
Southern - Southwestern wind
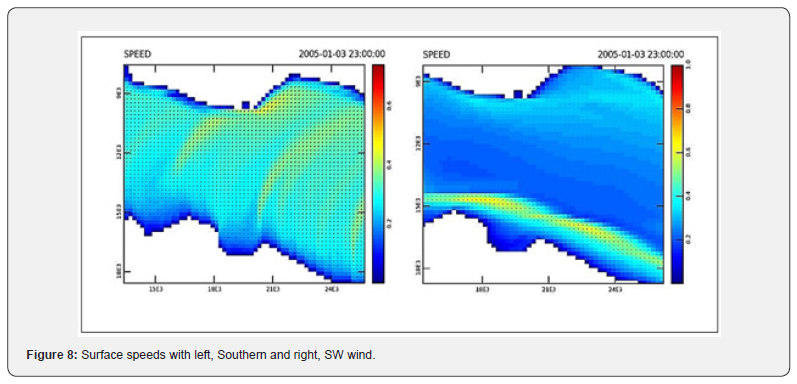
At the surface the southern wind creates currents with a Northeastern direction. The Southwestern wind creates strong currents on the northern but mainly on the southern coast of the bay.
To the south, there is a set-up on the north coast with a SW orientation. The bottom circulation is mainly to the north coast in an easterly direction and on the south coast to a westerly direction. The average circulation is very similar to the bottom circulation. With Southwestern wind there is there is a set-up on the coast with a western orientation (Buffalo Bay). On the bottom we have a reverse direction mainly in the centre of the bay while on the North and South coasts we have an Eastern direction. The average circulation is again similar to the bottom circulation.
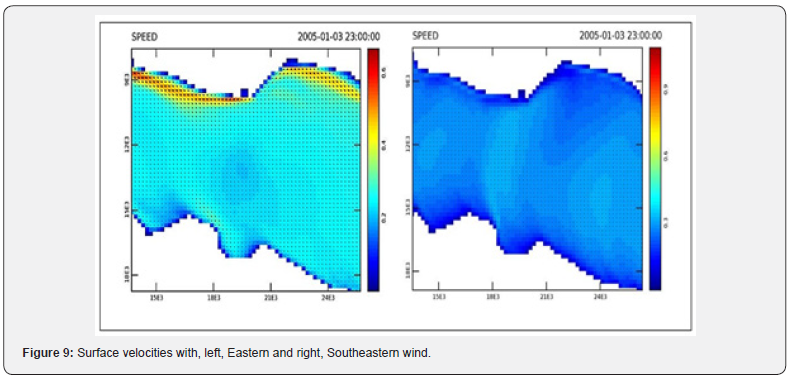
Eastern - Southeastern wind
At the surface, the easterly wind creates straight currents along the Northern shores in W and NW direction. The southeast wind creates a nearly uniform velocity field on the surface in a northerly direction. The Eastern wind creates currents on the North coast of approximately the same direction as the surface currents. There is a return to the East parallel to the south coast. With a southeasterly wind the bottom circulation is the reverse of the surface circulation, i.e. to the south. On the south coast it turns to the west.
Discussion
This modeling study aimed at recognizing and quantifying the patterns of the sea currents induced by wind forcing and the resulting circulation. 3D simulations with ELCOM provide a host of possibilities for physical investigation in simulating both real time, short-term, complex marine processes but also in simulating medium and long term processes. Although the main processes can be hypothesized from theory and accumulated experience, the quantification and magnitude of the phenomena is greatly enabled by the application of the 3D hydrodynamic and thermodynamic models. In general, the application of such models in various coastal and estuary environments for a variety of purposes has been proven to be not only plausible but accurate as well [9]. The focus each time depends on the purpose and scope of the research, but there always seem to be some unpredicted -or unthought of- findings.
One such finding of the current study is that all 3 Northern winds, that prevail in the study area occurring more than 63% of the time, and with higher intensities, induce a transport of finer bottom sediment from the shores of Attica to the shallower western part of the Gulf, and partially to the across shores of Evia on a never stopping ‘conveyor belt’. The basin bed layer of the southern Euboean Gulf consists of Holocene sediments that might extend to a thickness of 14 m, while the sea bottom is dominated by mud except for the shallow coastal areas, where the sand may reach up to 50% of its overall consistency [1]. According to published maps regarding the state of the shores in Greece the western shores of Euboea appear stable, contrary to the opposite shores of Attica that experience erosion. This finding remains to be studied further and proven, or unproven, but it exemplifies the capacity of the 3D hydrodynamic models to study and model marine sediment transport issues, albeit indirectly.
Conclusion
In all cases the average transport due to the generated currents is at 90º to the left of the wind vector, i.e. that of the Ekman bottom layer. The prevailing northern winds induce a gyre that carries finer bottom sediment from the shores of East Attica to the shallower part of the Gulf, towards Avlida, and partly to the shores of Euboea. The generated currents at the surface have velocities that vary depending on the wind direction and range from 20÷60 cm/s. At the bottom, compensatory currents develop with velocities of up to 5 cm/s. The adaptation of the sea circulation (the equilibrium state) to the surface due to the wind blast occurs in about 18-24 hours from the beginning of the episode. The bottom circulation seems to reach equilibrium earlier, at 10-14 hours. The cessation of the wind is followed by inertial oscillations that fully decay in about 5 days. The latter results are further supported by the analysis in the appendix.
Appendix: estimation of temporal and spatial scales [10]
Although numerical model simulation can extend and quantify our knowledge of the hydrodynamics of a marine region, the main physical processes must be known in advance. One of the reasons why this pre-estimation is necessary is the selection and tuning of the model. We will therefore attempt below to make an assessment of the main scales, both temporal and spatial, that characterize the marine circulation phenomena in the central part of the South Euboean Gulf.
The Coriolis effect
The Coriolis 'force', as we know, is the result of the rotation of the earth and causes the movements to be deflected to the right (left) in the northern (southern) hemisphere. We can weight this effect using the inertial radius rc and the inertial period Tcor.
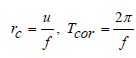
where f is the Coriolis parameter (f = 2Ωsinφ, Ω is the rotational speed of the Earth, Ω ≈ 7.2921*10-5 rad s-1 and φ is the latitude of the place, f = 8.9789*10-5 for latitude φ = 38º) and u (ms-1) is the speed of motion.
If the event in question (current motion, long-wave passage, etc.) is of a time period sufficiently shorter than Tcor, then there is 'not enough time' to deflect the direction of motion, while if the size of the basin is sufficiently smaller than rc then the Coriolis force 'does not have enough space' to turn the velocity vector. In the case under consideration we have the following magnitudes:
From the above table (Table 1) we conclude that for speeds such as those of sea currents (~0.2 m s-1) there will be a significant effect of the Coriolis force, as the width of the basin (Lwidth ~ 15 km) is much larger than rc, while for speeds such as that of a long wave (u = [gh]1/2 ~ 20 ms-1) there is no Coriolis effect.
The Rossby number, Rφ, expresses the ratio of the translational accelerations to the Coriolis accelerations, (which should be of the order of 0.1 or less for there to be a significant Coriolis effect) and the appropriate length, L, is the width Lwidth of the basin
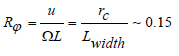

Ekman Currents
The estimation of the velocities and shape of sea currents caused by the wind blast can be done by Ekman's (1905) theory. This theory describes the currents in the upper layers of the sea in equilibrium under the influence of the wind shear stress and friction of the water layers during their movement, the Coriolis force, and the local pressure gradient (the slope of the water surface). The amount of motion is transmitted from the surface to the deeper layers through vertical turbulent mixing (eddy viscosity) with a constant (according to Ekman) coefficient Kz.
As is well known, the direction of the surface current forms a 45 degree angle to the right of the wind direction (in the northern hemisphere) and its speed (which at the surface is UE) decreases exponentially with depth. At depth z = hE the current direction turns in the opposite direction to that at the surface and the water velocity at this depth has decreased by exp(-π), at a rate of about 4.3% relative to the velocity at the surface UE.
This form is called the Ekman spiral. The main transport of water due to the current occurs at a depth z = hE /2 and is at an angle of 90 degrees to the right of the wind direction. Before establishing a free surface slope and at times shorter than the adjustment times (which we will discuss later) the sizes mentioned above are given by the following formula:
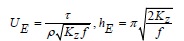
Where τ is the wind stress (Pa), ρ is the density of seawater (= 1027 kg m-3), Kz (m2 s-1) is the constant eddy viscocity coefficient. The wind tension τ depends on a coefficient C (Ekman used the value C = 0.0026), the air density ρa, ρa = 1.25 kg m-3, and U10 (m s-1) the air speed at a height of 10 m above the sea surface.
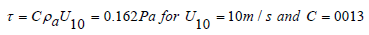
So, for a typical value of Kz = 10-3 m2 s-1
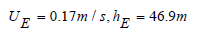
From the literature, Ekman used the following formulas
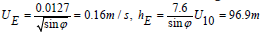
for UE10 = 10m/s
Observations and measurements since then have finally given a surface velocity equal to half that predicted by Ekman, while the thickness of the layer was measured in very good agreement with its predicted value. At the bottom, if there is some motion, an Ekman layer will also occur in reverse order to the surface layer. This layer is called the Ekman bottom spiral.
Time scale of current adaptation
Due to the inertia of the water the wind will start to shape the surface currents with some delay. The Coriolis effect will become noticeable after t > 0.25/f ~ 46 min. The adaptation period as a whole can be approximated as

where H may be the average depth of the basin assuming that the basin is fully mixed. If we assume H = 44m and Kz = 10-3 m2 s-1 we have T = 2.5 days approximately, while with Kz = 10-4 m2 s-1 we have T = 7.8 days approximately.
Stream structure in equilibrium
In closed basins the prolonged wind blow will create an elevation of the water surface in the downwind direction (wind set-up). Since this will create a pressure gradient, it will also cause a compensatory flow (return flow) which takes place in the deeper layers of the basin. This circulation is complex and depends on the topography of the seabed, possible stratification, wind conditions, etc. This flow will be generated within a long-wave travel time, i.e. within about 10 minutes for a distance such as that between Eretria and Oropos (L/u =7500/17=7.3 min).
An estimate of the level difference Δh in the direction Eretria - Oropos is
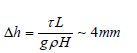
with H=30m, L=7500 m and τ = 0.162 Pa.
For an estimate of the velocity resulting from this level difference
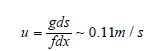
which is however considered to overestimate the actual velocity since it does not take into account the friction on the bottom.
Inertial Oscillations
If the wind suddenly deafens or changes direction then the process of adjusting the water flows under the influence of the earth's rotation to a new equilibrium state will be accompanied by oscillations around this new equilibrium position. These inertial oscillations have a characteristic period Tcor (~19h). The damping rate of these oscillations depends on their inertial period. The time scale of the adjustment of the currents to a new pressure gradient is t >> 1/f ~ 3 h. A good approximation is t~3÷5 Tcor, i.e. t ~ 2.3 to 4 days. For an estimate of the minimum adaptation time we can consider half the period of the single-node oscillation (seiche, see below).
It should be stressed that in case the basin depth is greater than hE a distinction between the two time scales should be made in order to adapt the currents to the surface layer. These time scales correspond to
a) Ekman adjustment due to Coriolis and frictional stresses in the Ekman layer
b) Inertial motion due to Coriolis and pressure gradients
It should also be mentioned that in case the wind stops we will have the creation of standing waves (seiches) in the basin (if it is closed). The period of these standing waves is given by Merian's formula:

where n is the number of nodes in the oscillation. For a single-node (n=1) oscillation we have Th = 12.6 min for the route Eretria - Oropos.
To Know More About Juniper Online Journal Material Science Please click on:
https://juniperpublishers.com/jojms/index.php
For more Open Access Journals in Juniper Publishers please click on:
https://juniperpublishers.com/index.php





No comments:
Post a Comment