Biostatistics and Biometrics - Juniper Publishers
Abstract
In this letter, a new and exact homogeneity test for real data is presented. It does not underlie any restrictions and is especially applicable in case of small sample sizes or pathological absolute or expected frequencies and generalizes the famous chi-squared test which is not an exact test.
Keywords: Hypothesis testing; New and exact homogeneity; Test for real data
Mathematics Subject Classification 2010 62G10
The electronic communication line sascha.woerz@wzw.tum.de which will change over the coarse of time to a unknown one which will be given in due coarse.
Introduction and short literature review
The famous chi-squared homogeneity test can only be applied to absolute frequencies and underlies some restrictions on the sample size, the absolute frequencies and the expected ones, where the former should be greater than 30, the absolute frequencies shall attain a minimum of 10 and the expected ones should be bounded from below by 1, where at least 80 percent of them should be greater than 5, see [1-14]. In this letter, the wellknown classes of goodness-of-fit-statistics including that of Freeman and Tuckey for testing discrete models [3] are generalized to continuous ones. In addition, the famous chi-squared homogeneity test is not exact [9,15]. While some attempts were made to improve the chi squared test for certain applications [4,5] by finding an adjusted statistic with a better chi-squared approximation or by minimizing chi-square distances under the hypothesis of homogeneity while introducing some optimality criteria distances and investigating their convexity properties resulting in an analytical solution for the optimal estimator under the hypothesis of homogeneity, in this letter, a new and exact test for real data is proposed. It generalizes the famous chi-squared test by assuming that the
chi-squared distribution with mn degrees of freedom. Especially, the
test does not underlie any restrictions as reported in [1,2]. Moreover, a
computational experiments is conducted.
Methodology
For the whole letter, assume ,.mnN∈ Suppose that the normally
be done in the following way:
Next, standardize the random variables
which is on the one hand exactly chi-squared distributed with mndegrees
of freedom and on the other hand represents the squared sum of absolute
standardized mean percentage errors.
Finally, the following hypothesis test is considered:
where 01α<< denotes the significance level.
Computational example
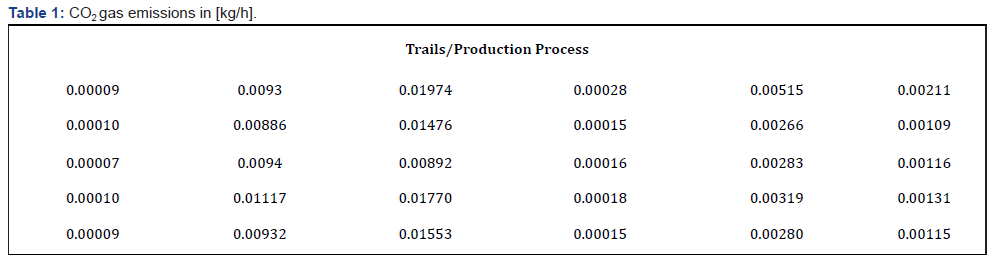
Consider the following CO2 gas emissions in [kg/h] originating from five different trials and six production processes (Table 1).
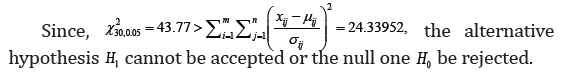
Conclusion
In this letter, the famous chi-squared test was generalized from discrete to continuous models with real data. A computational example which cannot be treated with the common chi-squared test showed that it can be applied in the same manner as the famous chi-squared test. In addition, the G-test [6] which is a likelihood ratio goodness-of-fit test can be generalized analogously, while results on the efficiency of chi-square and likelihood ratio goodness-of-fit tests can be found in [7]. A shell of nut tells: Since the new proposed homogeneity test does not underlie any restrictions since it is exact, it always performs better than the common chi-square and the G-test at the same computational cost with the addendum that it also can cope with real data.
To Know more about Biostatistics and Biometrics Open Access Journal
Click here: https://juniperpublishers.com/index.php
No comments:
Post a Comment