Biostatistics and Biometrics - Juniper Publishers
Abstract
Constrained Bayesian method (CBM) and the concept of
false discovery rates (FDR) for testing directional hypotheses is
considered in the paper. Here is shown that the direct application of
CBM allows us to control FDR on the desired level. Theoretically it is
proved that mixed directional false discovery rates (mdFDR) are
restricted on the desired levels at the suitable choice of restriction
levels at different statements of CBM. The correctness of the obtained
theoretical results is confirmed by computation results of concrete
examples.
Subject Classifications: 62F15; 62F03.
Keywords:
Directional hypotheses; Constrained Bayesian method; False discovery
rate; Mixed directional false discovery rates; False acceptance rate
Abbrevations: CBM:
Constrained Bayesian method; DFDR: Directional False Discovery Rate;
FDR: False Discovery Rates; MDFDR: Mixed Directional False Discovery
Rates; FAR: False Acceptance Rate
Introduction
The traditional formulation of testing simple basic
hypothesis versus composite alternative is a well studied problem in
many scientific works [1-8]. The problem of making the sense about
direction of difference between parameter values, defined by basic and
alternative hypotheses, is important in many applications [9-17]. Here
the decision whether the parameter outstrips or falls behind of the
value defined by basic hypothesis is meaningful. For parametrical
models, this problem can be stated as
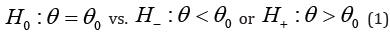
Where θ is the parameter of the model, 0θ is known.
These alternatives are called skewed or directional alternatives. The
consideration of directional hypotheses found their applications in
different realms. Among them are biology, medicine, technique and so on
[17,18]. The appropriate tests “has just begun to stir up some interests
in the educational and behavioral literature” [19-22]. Directional false discovery rate (DFDR) or mixed
directional false discovery rate (mdFDR) are used when alternatives are
skewed [17]. The optimal procedures controlling DFDR (or mdFDR) use
two-tailed procedures assuming that directional
alternatives are symmetrically distributed. Therefore, decision rule is
symmetric in relation with the parameter’s value defined by basic
hypothesis [14,23]. For the experiments where the distribution of the
alternative hypotheses is skewed, the asymmetric decision rule, based on
skew normal priors and used Bayesian methodology for testing when
minimizing mdFDR, is offered in Bansal et al. [17]. There theoretically
is proved “that a skewed prior permits a higher power in number of
correct discoveries than if the prior is symmetric”. This result is
confirmed by simulation study comparing the proposed rule with a
frequentist’s rule and the rule offered in Benjamini, et al. [23].
Because CBM allows us to foresee the skewness by not only a prior
probabilities but also by restriction levels in the constraints, it is
expected that it will give more powerful decision rule in number of
correct discoveries than existed symmetric or asymmetric in the prior
decision rules. Therefore, different statements of CBM, for testing
skewed hypotheses with restricted mdFDR, are considered below.
In Section 2 some possible statements of CBM for
testing directional hypotheses are considered and the fact that FDR
could be controlled on the desired level for each statement of CBM is
proved. Concretization of the proposed theoretical results for the
normally distributed directional hypotheses is given in Section 3.
Computation results of concrete example for normal basic and truncated
normal alternative hypotheses by simulation of the appropriate samples
are given in section 4. Discussion of the obtained results and made
conclusions are presented in sections 5 and 6, respectively.
CBM for testing directional hypotheses
Different statements of CBM for testing a set of
hypotheses are given in Kachiashvili, et al. [24]; Kachiashvili, [25];
Kachiashvili et al. [26]. They differ from each other by the kind of
restrictions put on the Type I or Type II errors made at testing. Let’s
introduce the following denotations for statement of the problem of
testing hypotheses [27]. Let the sample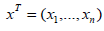 
be generated from (px;θ) and the problem of interest is to test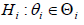 
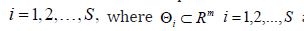are disjoint subsets with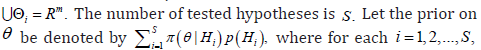 
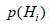iHpis the a priori probability of hypothesis 
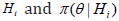is a prior density with support 
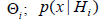denotes the marginal density of x given 
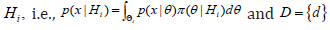is the set of solutions, where 
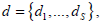it being so that
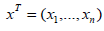be generated from (px;θ) and the problem of interest is to test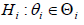 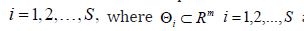are disjoint subsets with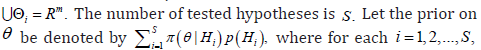 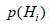iHpis the a priori probability of hypothesis 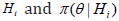is a prior density with support 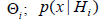denotes the marginal density of x given 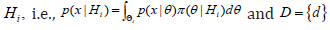is the set of solutions, where 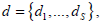it being so that 
associates each observation vector x with a certain decision 
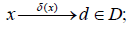
jΓ is the region of acceptance of hypothesis ,jH i.e.,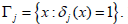 
It is obvious that δ(x) is completely determined by the jΓ regions, i.e. 
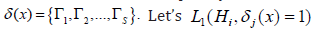and 
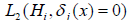be the losses of incorrectly accepted and incorrectly rejected
hypotheses. Then the total loss of incorrectly accepted and incorrectly
rejected hypotheses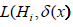 
is the following:
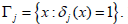It is obvious that δ(x) is completely determined by the jΓ regions, i.e. 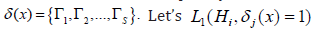and
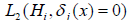be the losses of incorrectly accepted and incorrectly rejected
hypotheses. Then the total loss of incorrectly accepted and incorrectly
rejected hypotheses 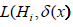is the following: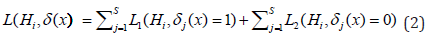
Adapting the made denotations to skewed hypotheses,
let’s consider some kind of CBM, from all possible statements, for
testing directional hypotheses (1). (Notation 1: numbering of the tasks,
described below, is preserved from Kachiashvili, et al. [27] 2.1.
Restrictions on the averaged probability of acceptance of true
hypotheses (Task 1). In this case, CBM has the following form
Kachiashvili, et al. [28]: to minimize the averaged loss of incorrectly
accepted hypotheses
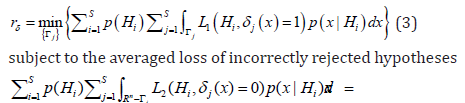
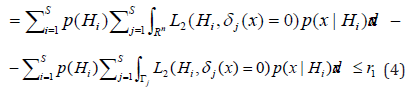
Where 1r is some real number determining the level
of the averaged loss of incorrectly rejected hypotheses. For directional
hypotheses (1) and loss functions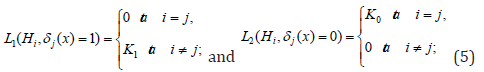 
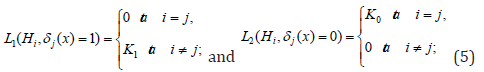
using concepts of posterior probabilities, the problem (3), (4) transforms in the following form Kachiashvili et al. [28]
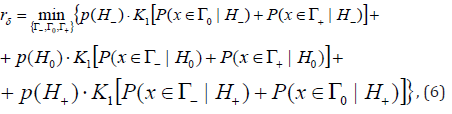
subject to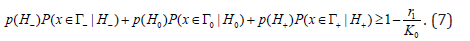
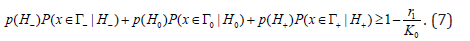
The solution of the problem (6) and (7) by Lagrange undetermined multiplier method gives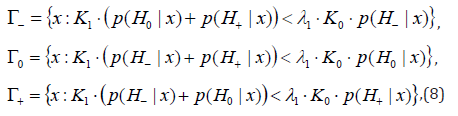 
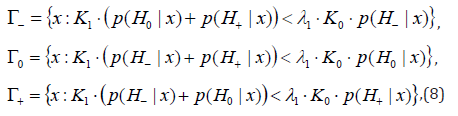
where Lagrange multiplier λ1 is determined so that in condition (7) equality takes place.
(Notation 2: for the statement (3), (4) as well as
for other statements (see Tasks 2, 4 and 5, below), depending upon the
choice of ,x there is a possibility that 1)(=xjδ for more than one j or
0)(=xjδ for all (),0,.
Let’s introduce denotations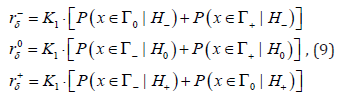 
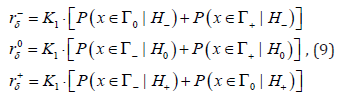
and let’s call them individual average risks. Then for the average risk (6) we HAVE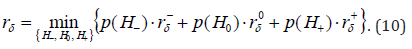 
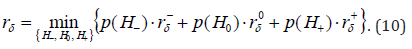
At testing directional hypotheses, it is possible to
make a false statement about choice among alternative hypotheses, i.e.
to make a directional error, or a type III error [23]. For recognition
of directional errors in the terms of false discovery rate (FDR) two
variants of false discovery rate (FDR) were introduced in Benjamini et
al. [29]: pure directional false discovery rate (pdFDR) and mixed
directional false discovery rate (mdFDR), which are the following
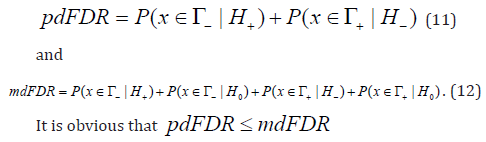
It is shown that the FDR is an effective model
selection criterion, as it can be translated into a penalty function.
Therefore, FDR gives the opportunity to increase the power of the test
in general case [30]. Both variants of FDR for directional hypotheses:
pdFDR and mdFDR can be expressed by Type III error rates (ERRIII):
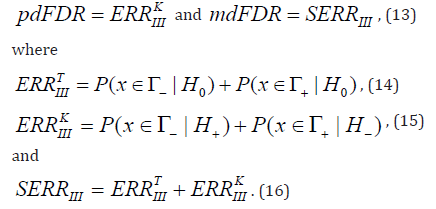
Here TIIIERR and KIIIERR are two different forms of
Type III error rates, considered by different authors Mosteller, et al.
[31]; Kaiser, [9]; Jones, et al. [13] and Shaffer, [14]) and IIISERR is
the summary type III error rate ()IIISERR [25].
Here in after, if necessary, let’s ascribe the number of the task related to the considered CBM directly to this abbreviation.
Theorem 1. CBM 1 with restriction level of (7), at satisfying a condition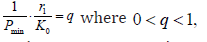 
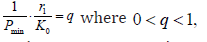
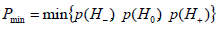ensures a decision rule with 
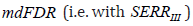less or equal to q i.e. with the condition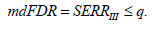 
Proof. Because of the peculiarity of decision making
rule of CBM, alongside of hypotheses acceptance regions there exist the
regions of impossibility of making a decision [26,32]. Therefore,
instead of condition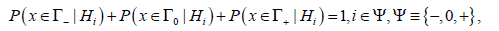 
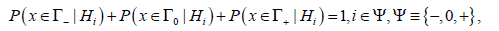
of the classical decision making procedures, the following condition is fulfilled in CBM
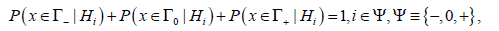
where imd is the abbreviation of the impossibility of making a decision
Taking into account (17), condition (7) can be rewritten as follows
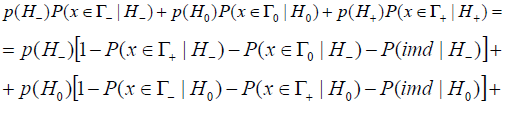
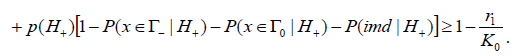
From here follows that
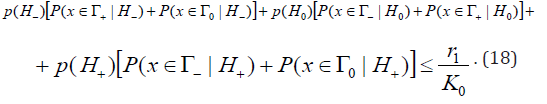
Let’s denote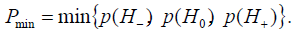 
Then from (18) we have
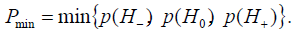Then from (18) we have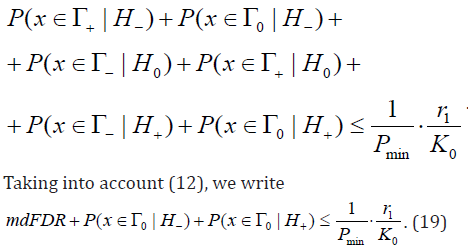
Taking into account (12), we write
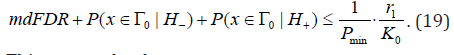
This proves the theorem
Let’s call false acceptance rate (FAR) the following
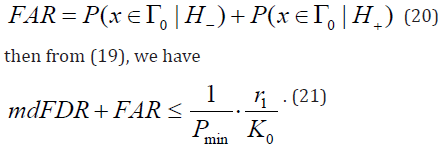
Restrictions on the conditional probabilities of acceptance of each true hypothesis (Task 2)
To minimize (6) subject to
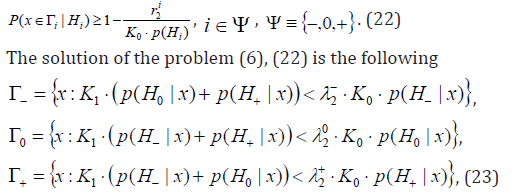
where Lagrange multipliers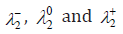 
are determined so that in conditions (22) equalities takes place.
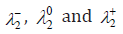are determined so that in conditions (22) equalities takes place.
Theorem 2. CBM 2 with restriction level of (22), at satisfying a condition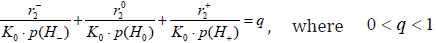 
q, ensures a decision rule with mdFDR (i.e. with IIISERR) less or equal to q, i.e. with the condition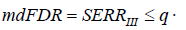 
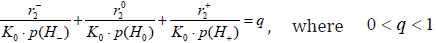q, ensures a decision rule with mdFDR (i.e. with IIISERR) less or equal to q, i.e. with the condition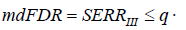
Proof. Taking into account (12), (17), condition
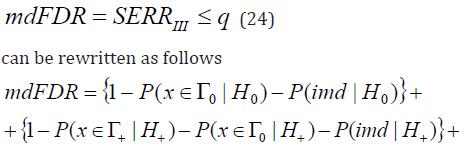
In our opinion these properties of and CBM are very interesting
and useful. They bring the statistical hypotheses testing rule much
close to the everyday decision-making rule when, at shortage of
necessary information, acceptance of one of made suppositions is
not compulsory.
The specific features of hypotheses testing regions of the
Berger’s test and CBM, namely, the existence of the no-decision
region in the test and the existence of regions of impossibility of
making a unique or any decision in CBM give the opportunities
to develop the sequential tests on their basis [2,36,26,28]. The
sequential test was introduced by Wald in the middle of forty of
last century [37,38]. Since Wald’s pioneer works, a lot of different
investigations were dedicated to the sequential analysis problems
(see, for example, Berger, et al. [39]; Ghosh, [40]; Ghosh, et al. [41];
Siegmund, [42]) and efforts to the development of this approach
constantly increase as it has many important advantages in
comparison with the parallel methods [43].
Application of CBM to different types of hypotheses (two and
many simple, composite, directional and multiple hypotheses)
with parallel and sequential experiments showed the advantage
and uniqueness of the method in comparison with existing ones
[24-29,44]. The advantage of the method is the optimality of made
decisions with guaranteed reliability and minimality of necessary
observations for given reliability. CBM uses not only loss functions
and a priori probabilities for making decisions as the classical
Bayesian rule does, but also a significance level as the frequentist
method does. The combination of these opportunities improves
the quality of made decisions in CBM in comparison with other
methods. This fact is many times confirmed by application of CBM
to the solution of different practical problems [45-47,32,44].
Finally, it must be noted that, the detailed investigation
of different statements of CBM and the choice of optimal loss
functions in the constrained statements of the Bayesian testing
problem opens wide opportunities in statistical hypotheses testing
with new, beforehand unknown and interesting properties. On the
other hand, the statement of the Bayesian estimation problem
as a constrained optimization problem gives new opportunities
in finding optimal estimates with new, unknown beforehand
properties, and it seems that these properties will advantageously
differ from those of the approaches known today.
In our opinion, the proposed CBM are the ways for future,
perspective investigations which will give researchers the
opportunities for obtaining new perspective results in the
theory and practice of statistical inferences and it completely
corresponds to the thoughts of the well-known statistician B
Efron [48]: “Broadly speaking, nineteenth century statistics was
Bayesian, while the twentieth century was frequentist, at least
from the point of view of most scientific practitioners. Here in
the twenty-first century scientists are bringing statisticians
much bigger problems to solve, often comprising millions of data
points and thousands of parameters. Which statistical philosophy
will dominate practice? My guess, backed up with some recent
examples, is that a combination of Bayesian and frequentist ideas
will be needed to deal with our increasingly intense scientific
environment. This will be a challenging period for statisticians,
both applied and theoretical, but it also opens the opportunity for
a new golden age, rivaling that of Fisher, Neyman, and the other
giants of the early 1900s.”
To Know more about Biostatistics and Biometrics
Click here: https://juniperpublishers.com/bboaj/index.php
To Know more about our Juniper Publishers
Click here: https://juniperpublishers.com/index.php
