On A Boundary Value Problem for A Singularly Perturbed Differential Equation of Non-Classical Type-JuniperPublishers

Journal of Biostatistics and Biometrics-Juniper Publishers

Abstract

In a semi-infinite strip we consider a boundary value problem for a non-classical type equation of third order degenerating into a hyperbolic equation. The asymptotic expansion of the problem under consideration is construction is constructed in a small parameter to within any positive degree of a small parameter.

Introduction

Boundary value problems for non-classical singularly perturbed differential equations were not studied enough. We can show the papers devoted to construction of asymptotic solutions to some boundary value problems for non-classical type differential equations [1-3].

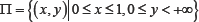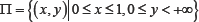In this note in the infinite semi-strip  we consider the following boundary value problem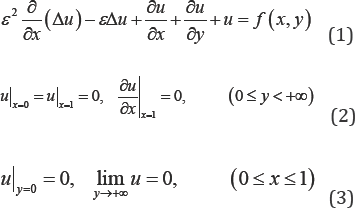

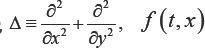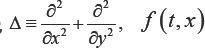Where &>0 is a small parameter, is the given function.

The goal of the work is to construct the complete asymptotics in a small parameter of the solution of problem (1)-(3). When constructing the asymptotics we follow the M.I. Vishik LA & Lusternik [4] technique.

The following theorem is proved.

Theorem

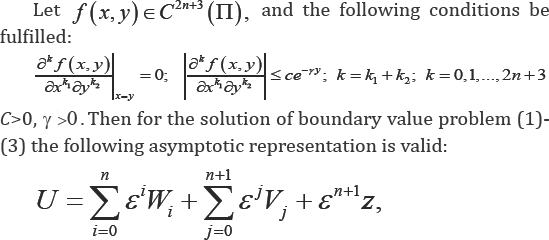
where the functions Wi are determined by the first iterative process, Vj are the boundary layer type functions near the boundary x=1 determined by the second iterative process, en+1 Z is a remainder term, and for z we have the estimation

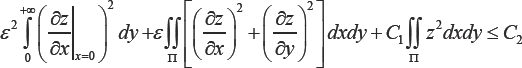
Where c1>0, c2>0 are the constants independent of e. References

To know more about Journal of Biostatistics and Biometrics

Click here: https://juniperpublishers.com/bboaj/index.php

To know more about Juniper Publishers

Click here: https://juniperpublishers.com/index.php