Biostatistics and Biometrics Open Access Journal

Abstract
A three state Markov Chain Model is used to determine the pattern of gene distribution on Albinism. We assumed that one of the parents (first parent) must be normal Homozygote person and the forces behind evaluation are brought to bare. This paper discovered that after six generations, the gene of the Albino will no longer be present in the population as all will be normal homozygote individuals.
Keywords: Mathematics Modelling; Markov Chain; Albinism; Autosomal Recessive
Abbreviations: ARD's: Autosomal Recessive Diseases; aa: Homozygote Affected; Aa: heterozygote affected; AA: Homozygote Normal
Introduction
Selection is one of the evolutionary forces which promotes adaptation and keep in checks the disorganizing effects of the order processes. Natural selection may be due to differential survival or differential fertility or both. According to Hoppensteadt & Peskin [1] that Fisher in his fundamental theorem of Natural selection in 1930 established a direct correlation between the amount of genetic variation in a population and the rate of evolutionary changes by natural selection mathematically with respect to fitness. Choji & Garba [2] established that the rate of increase in fitness of a population at any given time is equall to its genetic variation in fitness at the time. Relative fitness predicts the course of selection, that is, it predicts how gene frequencies will change Choji & Edemanang [3].
Autosomal recessive is one of the several ways that a trait or disorder is passed down through families. If a disease is Autosomal Recessive, it means you only need to get the abnormal gene from one parent in order for you to inherit the disease. One of the parents may afterwards have the disease. Furthermore, because a recessive deleterious gene produces its disease only in the homozygote, affected individuals must receive one mutant gene from each parent. Consequently, since recessively inherited diseases are usually rare in the population almost all homozygous affected individuals aroused from the mating of two heterozygous unaffected parents. Example of such Autosomal Recessive Disease are sickle cell anaemia, albinism etc. Myriad of researched carried on the reduction/control of Autosomal Recessive Diseases (ARD's) where tilted on the medical and biological aspect, as demonstrated by James & Clarke [4], Fred [5]. Nowadays, researchers are approaching the problem from mathematical point of view, the work of Choji & Edimanang [3] , Choji & Garba [2] gives another insight in approaching the problem, with more worked still to be done.
Albinism is a hereditary defect in the metabolism of melanin requiting in the congenital absence or major decrease of pigmentation in the skin, mucosa, hair and eyes. It is an Autosomal Recessive Disease that a career (that is a person carrying the gene/trait) can pass on to his next generation. Mathematical modelling has been observed along the years to play an essential role in science. Typically, one may give a state of the system at an initial time, and may be required to find out the state of the system at some future time. A typical model used for such situation is the Markov Chain model. Markov Chain Model can be used to characterized a sense of experiments in which the outcome of each experiment will depend only on the outcome of the immediate preceding experiments Choji & Garba [4].
Methodology
Markov chain model
A Markov chain model is one of the vital tools used in stochastic process. The construction of Markov chain require two basic ingredients namely a “Transition Matrix” and an “Initial Distribution" [6]. So by definition of the transition matrix, we assume a finite set S, where = {1,..,m} are the m-states. Assign to each pair (i, j)òS2 of states a real number Pij such that the properties.
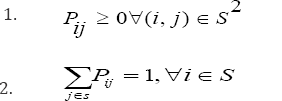
Are satisfied and define the transition matrix P by

Let (Xn)n ϵ N0 be a sequence of random variable with values in S. Here, n denotes the time at which the state Xn occurs. So far, we have only specified the ingredients for the evolvement of probabilities throughout the time. To complete the construction of Markov chain, we denote Ds as the set of discrete distributions on S, such that
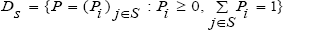
Where we represent distribution as row vectors. We call P0 = (P0i)iϵS ϵ Ds the initial distribution of the chain {χn }nϵN0 if P [X0=1] = P0i, ∀states i ϵ S
A discrete time Markov process is completely described by its square transition matrix P.Pij means that the probability of transition from state i to state Pi(0) j, implies that the probability of the system being in state 1 at time t = 0. The probability that the system in state 1 at t = t0 is given by
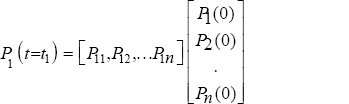
In general, we can write
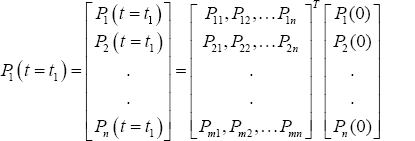
Where T indicates the transpose of the matrix or vector as the case may be Choji & Edemanang [3]. Probability state vector is a vector composed of state probabilities, which sum up to 1. A state is a situation that a process can assume at any given time and are mutually exclusive and exhaustive. If for instance pi (0) = 1 then pi (0) = 0 for i ,j = 1 ,2 ,3 and for I, j. Transition is matrix of conditional probabilities of moving from one sate to another. Subsequently, probability state vectors (PSV) can be obtained as follows
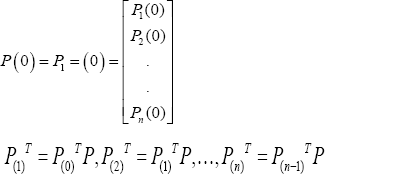
The Markov chain model for a three transition is given below
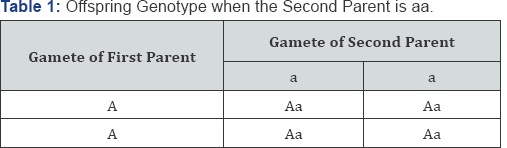
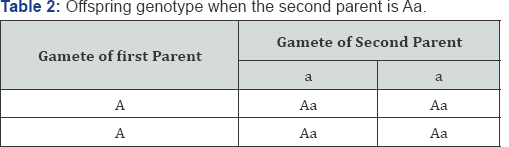
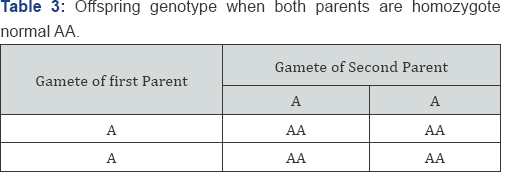
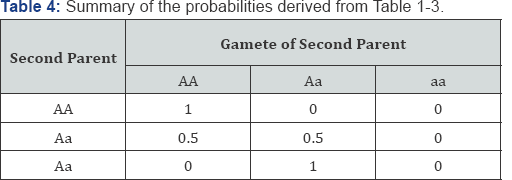
From Table 1 above, it is observed that when one of the parent is homozygote normal (AA) and the other is homozygote affect (aa), all the offspring will be heterozygote (Aa) but affected with the traits since the trait is autosomal recessive. We discovered from Table 2, that when one of the parent is normal (AA) and the other is heterozygote, Half of all the offspring will be heterozygote (Aa), and half will be normal (AA). From Table 3 above, we notice that when both parents are normal (AA), all the offspring will be normal with probability of 1. Table 4 above shows the probability of an offspring being in one of the three genotypes. For each possible genotype of the second parent, when the second parent is married to a homozygote normal first parent (AA), the probabilities take a matrix form as follows
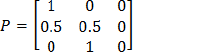
Experimented result
Numerical experiment: Let's consider a settlement that may have the following initial probability state vectors (IPSV) [0.2,0.3,0.5],[0.1,0.4,0.5]and[0.6,0.3,0.1] respecting P(1)T = P(0)TP for first generation p(i)T = p(i-1)TP and for any other generation , we obtained the data shown in the tables below for the probability state vector (PSV) movement pattern for the three genotypes.
Discussion & Results
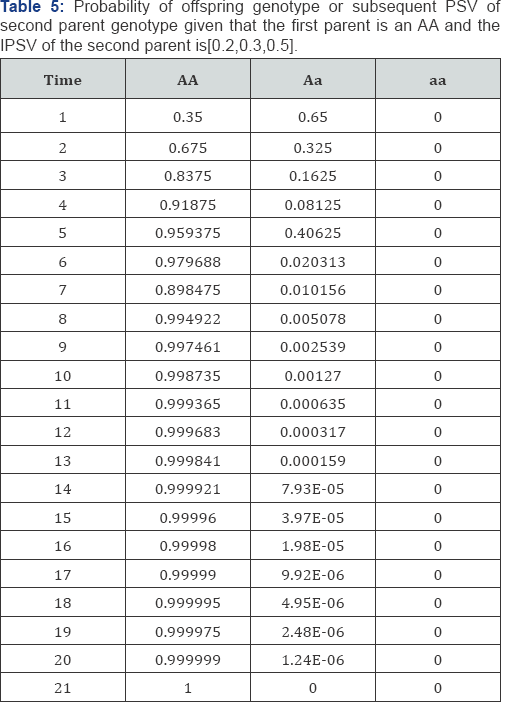
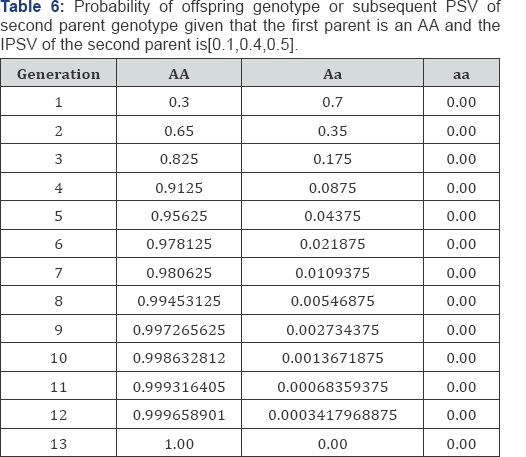
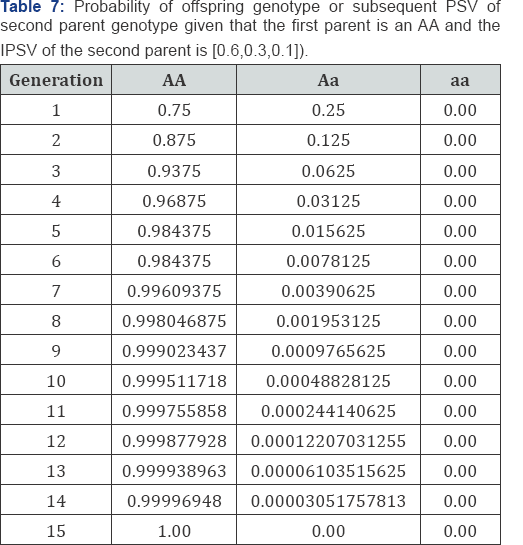
From Table 1 above, it is observed that when one of the parents is homozygote normal (AA) and the other is homozygote affected (aa), all the offspring will be decisive. While in Table 2 half of the offspring will be heterozygote affected (aA) and half will be homozygote normal (AA) We discovered from Table 2, that when one of the parent is normal (AA) and the other is heterozygote, Half of all the offspring will be heterozygote (Aa), and half will be normal (AA). Similarly, we also observed in Table 3 that the offspring will be normal (AA) with probability of one (I) when parents are normal (AA). The result in Table 4 & 5, shows that equilibrium is reached after 12 generations for the probability of offspring genotype given that the first parent is [0.2,0.3,0.5] . And from Table 6, the result also indicates that equilibrium is attained after 12 generations for the probability of offspring genotype given that the first parents are . Consequently, in Table 7 the result also indicate that equilibrium is reach after 12 generations for the probability of offspring genotype given that the first parent is [0.1,0.4,0.5]
Conclusion
From the analysis, it is observed that in less than 12 generations, equilibrium is attained in the three instances. Also, in about six generations, the gene of albino was eliminated from the genotypes of the settlement. Under the condition given, it is obvious that whenever the initial probability state vector, the gene of albino will no more be in existence after the generation. This is true since each probability state vector tends to [0.0,0.0,00] . The result of the study shows that, after six generations, the population acquired a normal homozygote. Therefore, the three states Markov shows that after a number of generations, all people in the settlement will be homozygote normal.




No comments:
Post a Comment