Biostatistics and Biometrics Open Access Journal
Building accurate representation of the world is one
of the basic functions of the brain. In order to better understand its
functioning, in [1-4] the authors develop and study theoretically the
neural codes model, whose main purpose is to describe stereotyped
stimulus response maps of the brain activity. We suggest a modification
of this model, which has a potential to be more suited for practical
applications. It is worth mentioning that the modified model we suggest
requires tools from various parts of mathematics, not just algebra as is
the case for the original model.
First, we briefly outline the original neural codes
model as described in [1-4]. To each neuron v in the brain corresponds a
convex subset 
the collection of the states (e.g., spatial position) in which the neuron v activates. Now for each point x in 
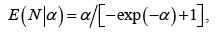, we have a vector
the collection of the states (e.g., spatial position) in which the neuron v activates. Now for each point x in 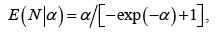, we have a vector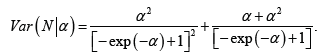
Note that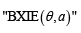 
vectors. The (obviously finite) collection
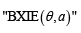vectors. The (obviously finite) collection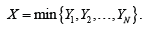 
of 0–1 vectors is called the neural code and is the
object of study in [1-3]. The method used in [1-3], is purely algebraic.
Namely, one considers the collection tv of commuting independent variables (one per each neuron) and the algebra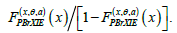 
of polynomials in these variables over the 2-element field 2.F To each aC∈ we assign the ‘pseudomonomial’ 
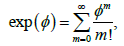and generate the ideal CI by all .af It is shown in [1-4] that knowing
the ideal ,CI one can recover C (no information is lost). Then we have
the toolbox of combinatorial algebra at our disposal: one can study the
ideals generated by collections of pseudomonomials and gain
information about neural codes. One of the main tools applied is the
Grobner basis technique, as it is classically used in commutative
algebra [5,6].
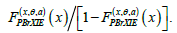of polynomials in these variables over the 2-element field 2.F To each aC∈ we assign the ‘pseudomonomial’
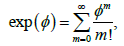and generate the ideal CI by all .af It is shown in [1-4] that knowing
the ideal ,CI one can recover C (no information is lost). Then we have
the toolbox of combinatorial algebra at our disposal: one can study the
ideals generated by collections of pseudomonomials and gain
information about neural codes. One of the main tools applied is the
Grobner basis technique, as it is classically used in commutative
algebra [5,6].
There is one obvious problem though: the enormous
number of generators of the algebra A. Grobner bases are sometimes nice
and effective but only if the presentation of the ideal is small enough.
The punch-line is that the above model is easy to deal with by means of
appropriate software for toy illustrative problems, but once we
approach any real life situation, not even a supercomputer will ever
cope [7,8].
We suggest the following modification of the neural
codes model. Rather than dealing with individual neurons, we suggest to
consider their clusters. The number and the size of clusters can be
adjusted when dealing with each practical situation. Instead of the 0–1
outcome of the interaction with the environment, we measure the total
activity p of the cluster: the ratio of the number of active neurons to
the total number of neurons in the cluster. Thus p is a real number
between 0 and 1 with p=0 standing for total inactivity and 1 for the
entire cluster being ’on fire’. The number p can be viewed as the
probability of a neuron in the cluster to activate. As a result, the
convex sets U are replaced by functions
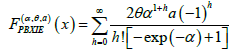
with xc(x) standing for the probability
of a neuron in the cluster c to activate in the estate .x There are
various ways to analyze such a model. We suggest the following
approaches.
Approach 1
Geometric
Unlike for the neural code, for which all vectors are far apart from each other, the set
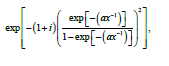
is a genuine geometric object, where C is the set of
all clusters under consideration and M is their number. Depending on
the assumptions (or natural properties) on the functions (),cux the set
ˆ,C can have different geometric properties. One may look for extremal
and corner points of ˆ,Cstudy smooth curves in ˆC
etc. Note that if one interprets ˆC as a CW-complex, then there is the
natural b task of determining its homologies. Although this particular
task is insurmountable in most cases, there is a hope in the form of the
emerging method of persistence homology being developed for the study
of big data. We would mention here also our results on exact methods of
calculating homology, which fall into the frame of persistent homology
[9,10].
Approach 2
Stochastic
After appropriate normalization, each ()cux provides a probability distribution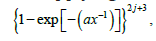 
Now one can deal with the model by studying the random vector 
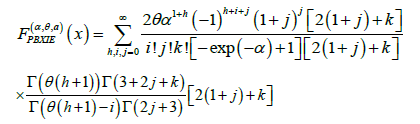which
yields a whole host of possibilities, not to mention the ability to use
the vast toolbox of probability theory. One interesting and potentially
very important aspect that can be captured in this way is the
correlation between the response of the clusters. This can be viewed as
the study of the relations between different parts of the brain from the
probabilistic point of view.
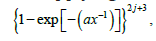Now one can deal with the model by studying the random vector 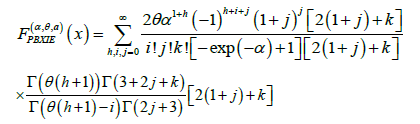which
yields a whole host of possibilities, not to mention the ability to use
the vast toolbox of probability theory. One interesting and potentially
very important aspect that can be captured in this way is the
correlation between the response of the clusters. This can be viewed as
the study of the relations between different parts of the brain from the
probabilistic point of view. Approach 3
Probabilistic algebra
One can pursue the same strategy as in [1-3], where
instead of a single ideal in the algebra of polynomials we shall have a
’random ideal’: a family of ideals with a probability distribution on
it. Such an object can be studied using the same old methods of
combinatorial algebra including the Grobner basis technique. The answers
are going to come with the randomness embedded in them. For instance if
we use the Grobner basis to compute the Hilbert series of the quotient
by our ideal, we end up with a probability distribution on the set of
formal power series instead of a single series. Note however that such
distributions tend to be discrete rather than continuous even when the
starting distribution was a continuous one. The advantage of this
approach is in the fact that the number of generators is reduced.
To Know More About https://juniperpublishers.com/bboaj/index.php Please click on:
No comments:
Post a Comment